以下的分析将帮助用户理解进化如何成为一种双倍指数增长的现象(也就是说,指数增长中的指数增长速度(指数)本身也在以指数速度增长)。尽管这里的公式与进化的其他方面相似,但是我将在后面的内容中描述计算能力的增长,特别是基于信息的过程和技术,其中包括人类智能的知识,它是软件智能的主要源头。
我们将关注以下三方面内容:
V:计算(以每单元造价每秒产生的计算能力衡量)的速度(这里是指能力)
W:用于设计和构建计算设备的世界知识
t:时间
在第一级的分析中,我们通过W的一维线性函数审视计算机能力。我们还注意到W在不断累积。这是由相关的技术算法以增量的方式累积为基础。就人脑而言,进化心理学家认为大脑是一个巨大的模拟智能系统,并且随着时间的流逝以增量的方式进化。同样在这个简单的模型中,瞬间增加的知识与计算能力成正比。通过观察得到的结论随着时间的增长,计算能力呈指数方式增长。
换言之,计算机的能力就是用于构建计算机的知识的线性函数。这实际上是一个保守的估计。总之,创新是通过很多种方式而非附加的方式来提升V值的。独立的创新(每一次创新代表着知识的线性增加)将成倍地提升彼此的效果。例如,CMOS(互补金属氧化物半导体)是电路技术的一项进步,它是一种高效的集成电路布线方法;流水线是处理器的一项重要创新;傅里叶快速变换是一种算法的改进;所有这些都是通过独立相乘的方式增加了V值。
在开始阶段,我们可以观察到:
计算的速率正比于世界的知识:
(1)V=c1W
世界知识改变的速率正比于计算的速率:
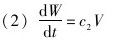
将(1)带入(2),可得:
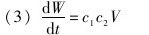
进一步可以得到:
(4)W=W0e(c1c2l)
W将随着时间以指数速度增长(e是自然对数的底)。
数据显示将以指数增长的方式增长(在20世纪早期,计算机的能力以每3年的时间翻倍;20世纪中叶,计算机能力翻倍所需时间为2年;现在计算机能力每年都会翻倍)。技术的指数增长能力导致了经济的指数增长。这是从过去一个世纪得出的结论。有意思的是,经济萧条(包括20世纪30年代的经济大萧条)以弱周期出现于潜在的指数增长之上。在每次经济萧条后,经济又得到了迅速恢复,似乎经济萧条和衰退从来就未曾发生过。我们可以看到某些特定行业呈更快的指数增长趋势,这些行业与那些指数增长的技术相关联,如计算机工业。
如果将指数增长的资源作为计算的重要因素,我们可以看指数增长的第二层次:让我们来再看下面的公式:
(5)V=c1W
现在包含用于计算的资源部署N:
(6)N=c3e(c4t)
现在世界知识的变化率与计算速度和部署的资源的乘积成正比:
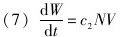
将(5)和(6)带入(7)可得:
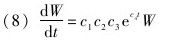
进一步可以得到:
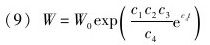
世界知识就以两倍的指数增长速率累积。
现在让我们考虑现实世界中的数据。在第3章中,我估计了人脑的计算能力,基于对人脑所有区域功能模拟的需求估算,人脑的计算能力为1016cps。模拟每个神经元和神经元间连接间的突触的非线性需要更高数量级的计算。1011的神经元乘以每个神经元(计算主要发生于这些连接中)103的连接,乘以每秒102事务处理,再乘以每次事务处理需要的103计算——总共的计算能力为1019cps。下面的分析假设了功能模拟的计算级(1016cps):
分析3
考虑20世纪的实际计算设备和计算机的数据:
令S=cps/$1K:花费1000美元获得的每秒的计算能力。
20世纪的计算数据由以下公式计算:
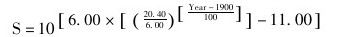
假定一段时期的增长率为G,可得:
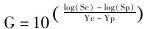
Sc是当年的cps/$1k,Sp是之前某年的cps/$1k,Yc是当年的年份,Yp是之前某年的年份。
人脑=1016cps
人类种族=100亿个人脑=1026cps
2023年我们能够用1000美元达到人脑的计算能力(1016cps)。
2037年我们能够用1美分达到人脑的计算能力(10 16cps)。
2049年我们能够用1000美元达到整个人类的计算能力(1026cps)。
如果我们考虑经济指数增长的因素,特别考虑到可用的计算资源(已经达到了每年1万亿美元),在21世纪中叶之前,非生物智能将比生物智能强大数十亿倍。
我还可以通过另外的方法推导出双倍的指数增长。从以上的论述可以看出知识增加的速率至少与当时的知识呈正比。这清晰地表明很多更新(知识的增加)是以“乘法”的方式而非“加法”的方式增长的。
尽管如此,我们还是能够得到如下指数增长公式:
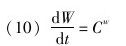
其中C>1,可以得到以下结论:
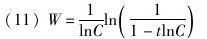
当t<1/lnC时,W以较慢的对数增长,但是当达到奇点,即t=1/lnC时,W将爆炸式地激增。
甚至对于最缓和的模型dW/dt=W2,同样将导致奇点的到来。
事实上任何能力增长法则都遵循以下的形式:
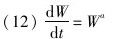
其中a>1,如此便得到在时间T关于奇点的另一个解决方案:
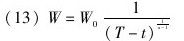
a的值越大,越接近奇点。
在我看来,很难想象依据有限的知识,并考虑到非常有限的物质和能量资源,可以计算出达到指数双倍指数增长过程的日期。增量(如W)看起来可以是如下形式W*log(W)。它描述了网络影响。如果我们有一个类似于互联网的网络,它的影响或价值将正比于n*log(n)。鲍勃·梅特卡夫(以太网的发明人)认为有n个节点的网络的价值等于c*n2,但其价值被过于夸大了。如果互联网的规模增倍,其价值也会增加,但不会成倍增加。一种合理的估计是,网络对于每个用户的价值将正比于对网络规模取自然对数值。故网络的价值将正比于n*log(n)。
如果在增长速率时引入对数网络的影响,我们能够获得如下速率变化的等式:
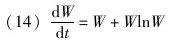
如此,双倍指数增长的解决公式变为:
(15)W=exp(et)
