首先我们先想一下什么是“时间”,怎么定义这个词。你很快就会发现这个词很难定义,在做了各种试图定义它的尝试之后,我们不得不承认,我们总是会陷入不得不用时间来定义时间的逻辑怪圈。最后会发现,借助一个外部衡量工具来描述时间,可能是一个避免落入逻辑怪圈的最好方法。比如说一个钟摆,摆动一个来回我们就认为这代表过去了一秒,但是钟摆这种东西不够精确,误差太大,我们不能对这样的外部衡量工具满意。现在,让我们借助强大的思维实验和光速不变原理来构造一个宇宙中最理想、最精确的计时器,我把这个计时器叫作“光子钟”。下面看一下这个光子钟长什么样:
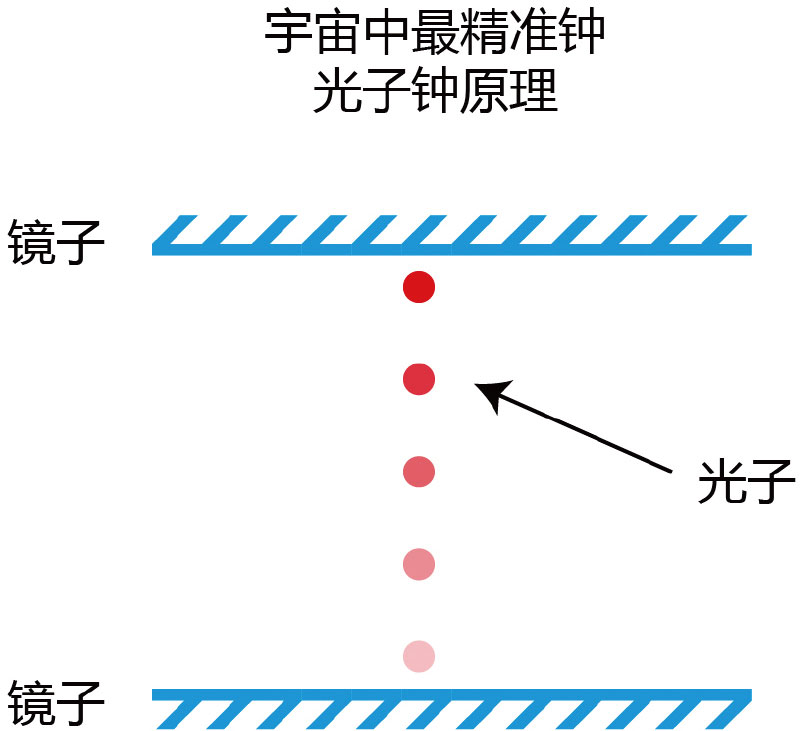
【图4-5】光子钟原理图
这个光子钟的构造非常简单,但是很实用。上下两面镜子相距15厘米,中间有一个光子可以在两面镜子中间来回地反射折腾。光子在两面镜子中间来回弹一次,可以想象成“嘀嗒”一声。我们已经知道光速是恒定不变的30万千米/秒,那么就很容易计算出,这个“嘀嗒”一下的时间是十亿分之一秒,换句话说,“嘀嗒”10亿次就代表时间走过了1秒。现在有了这个强大的光子钟,就不需要太纠结于时间的定义了,于是我们达成共识,通过“嘀嗒”的次数来衡量和比较时间这个虚无缥缈的东西。好了,现在你拿上这个光子钟坐上宇宙飞船,发射,你飞了起来。而我也拿着一个光子钟,站在地面上,看着你的宇宙飞船从眼前飞过。注意,既然是思维实验,我就想象我拥有神奇的能力,能够看清你手上那个光子钟的情况。现在我把这个情况画出来,你看是不是这样:
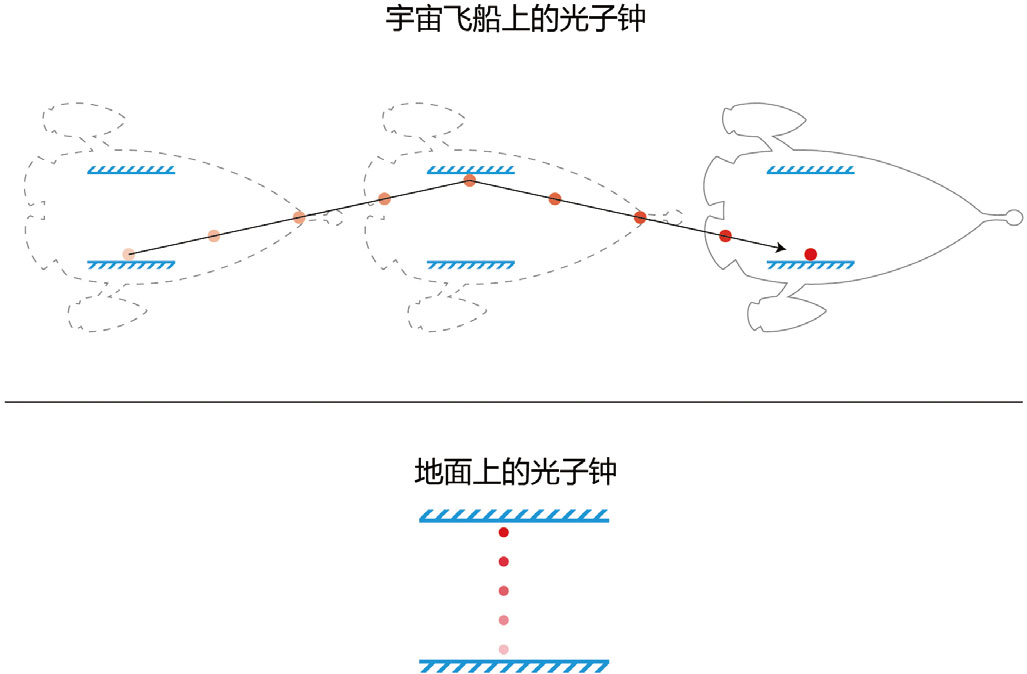
【图4-6】地面上的观察者看到的宇宙飞船中的光子飞行路线比地面上的要长
请开动你的脑筋,我保证本书中需要你像现在这样动脑子的地方很少,但无论如何这都是最关键的一次,这次想明白了,以后别处再遇到类似的图全部都可以轻松跳过,扫一眼就知道怎么回事。当我手上的光子钟在来回折腾时,你的飞船就会从A位置飞到B位置,那么我将会看到你手上那个光子钟里面的光子走过的是一条斜线。这是显而易见的,如果光子飞过的路径在我眼里不是斜线的话,光子必定飞到光子钟外面去了。现在我们运用光速不变原理来看一下,由于宇宙飞船上的光子飞行的路线比我手里的光子更长了,那么也就意味着,当我手里的光子钟“嘀嗒”一次的时候,飞船上的光子钟还来不及“嘀嗒”一次呢。换句话说,当我手里的光子钟“嘀嗒”了10亿次的时候,我看到飞船上的光子钟可能只“嘀嗒”了5亿次(打个比方,不要纠结5亿次是怎么算出来的)。根据我们前面已经达成共识的对时间最自然的定义,我得出这样的结论:在宇宙飞船上,你的时间过得比我慢!
或许你还是觉得不放心,你会想:“你用的是光子钟这种我从来没见过的东西,我还是对我自己的劳力士比较放心一点。”好吧,那么我们现在就拿你的劳力士来做实验吧,我们把飞船也换成你更熟悉的火车,这样你就更放心了吧。现在你坐在一列火车里,左手一只钟(光子钟),右手一只表,火车在做着匀速直线运动,窗户外面黑漆漆一片,你完全不知道自己是静止的还是运动的,那么你觉得你能用观察光子钟或劳力士的走时情况,来知道火车是静止的还是开着的吗?根据我们前面已经阐述过的爱因斯坦的相对性原理(在任何惯性系中,所有物理规律保持不变),你不可能靠任何实验的方法来确定自己的运动状态。反过来想,在一间密闭的车厢中,如果你能观察到光子钟和山寨劳力士走时忽然一样,忽然又不一样,那才是咄咄怪事呢。
我们在这里谈论的是时间本身变慢了,不是任何机械的或者化学的原因,就是时间本身变慢了,与时间有关的一切都变慢了,用一个很酷很形象的说法就是——时间膨胀了。还是回到刚才那个宇宙飞船的实验,在地面上的我会看到,不光是你的光子钟变慢了,你的动作、你眨眼的速度、你的新陈代谢、你一切的一切都变慢了。于是,你现在开始感到震惊了。趁着你现在精神好,赶紧让我们来计算一下,时间变慢的尺度和飞船的速度是什么关系呢?这个计算要用到我们非常熟悉的勾股定理,直角三角形的两个直角边和斜边的关系式:a2+b2=c2。
我们把刚才那个你坐宇宙飞船的景象再次画出来:
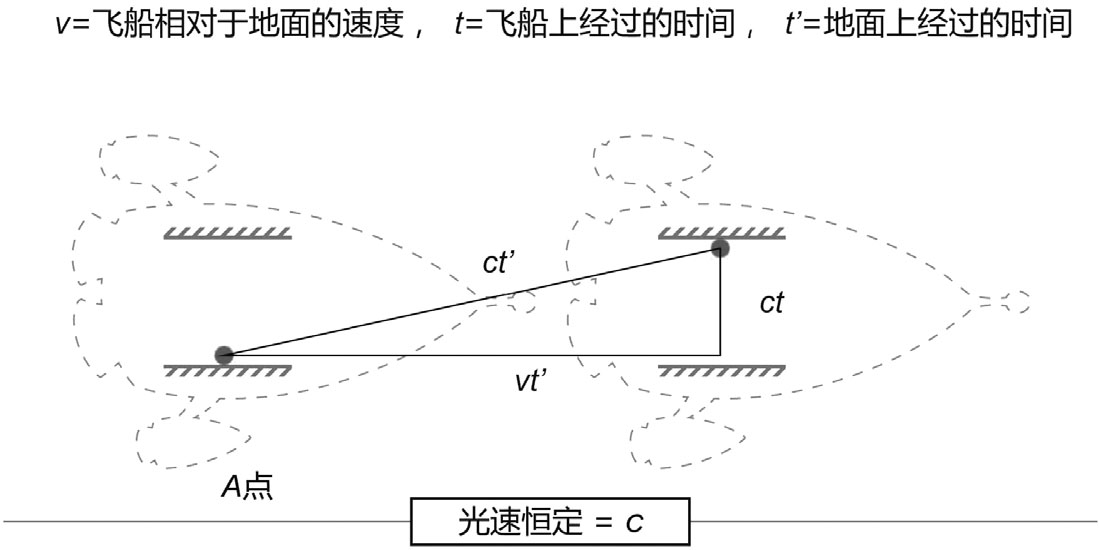
【图4-7】利用勾股定理可以推导出相对论因子
我在上面画了一些辅助线,并且用一些字母来表示飞船上经过的时间、地面上经过的时间、飞船相对于地面的速度和光速。注意那个t和t',我们曾经在本书刚开始没多久见过这个一撇。上面那个三角形的两个直角边分别是vt'和ct我估计你很容易理解,只是斜边为什么是ct'呢?这就是说从我(地面上的人)的角度来观察的话,光子以恒定速度c在地面上经过的时间t'走过的距离刚好是那个直角三角形的斜边。下面我们利用勾股定理写出这样一个等式。
(ct')2=(ct)2+(vt')2
接下来我们用一点最基础的方程变换的知识,来做点公式变形,我们的目的是要算出以地面为参考系时飞船上经过的时间t和地面上经过的时间t'之间的关系式:
第一步,先把括号都去掉:
c2t'2=c2t2+v2t'2
第二步,两边同时减去v2t'2
c2t'2-v2t'2=c2t2
第三步,两边同时除以c2
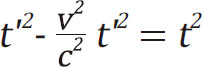
最后一步,整理成最终形式
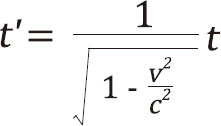
结束。
如果你顺着我上面的步骤一步步下来,毫无阻碍地得到了最终形式,那么请你深吸一口冷气,因为你发现了这个宇宙中一个最深刻的奥秘,这是迄今为止让人类第一次感到深深震撼的等式,这一刻,我们根深蒂固的时间观念崩塌了。
让我们凝视这个等式十秒钟,解读一下它的含义。
当v的速度相比光速很小的时候(比如汽车、火车甚至飞机速度都不及光速的百万分之一),则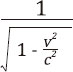 约等于1,这个公式就退回到了我们熟悉的伽利略变换式t=t',但如果我们的速度能达到光速,则t'等于无穷大。时间等于无穷大?怎么理解?这就是说随着运动速度的增加,时间会变得越来越慢,最后慢到了停止的地步。假如我们的速度能超过光速呢?那就不得不面临一个负数的平方根,大家知道这叫虚数。那这个虚数用在时间上表示什么?难道这就是传说中的穿越?哦,不,这不代表时光倒流,虚数没有现实意义,事实上我们后面马上就要证明达到或者超过光速都是不被允许的,本书将在第五章跟大家讨论关于时空穿越的可能性,但那也绝不是通过超光速来实现的。请不要着急,这次奇妙的时空旅程才刚刚开始,还有很多奇景等待你前去观赏。
约等于1,这个公式就退回到了我们熟悉的伽利略变换式t=t',但如果我们的速度能达到光速,则t'等于无穷大。时间等于无穷大?怎么理解?这就是说随着运动速度的增加,时间会变得越来越慢,最后慢到了停止的地步。假如我们的速度能超过光速呢?那就不得不面临一个负数的平方根,大家知道这叫虚数。那这个虚数用在时间上表示什么?难道这就是传说中的穿越?哦,不,这不代表时光倒流,虚数没有现实意义,事实上我们后面马上就要证明达到或者超过光速都是不被允许的,本书将在第五章跟大家讨论关于时空穿越的可能性,但那也绝不是通过超光速来实现的。请不要着急,这次奇妙的时空旅程才刚刚开始,还有很多奇景等待你前去观赏。
现在我们已经掌握了这个时间变换的神奇公式:
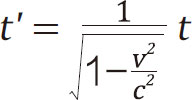
为了让这个公式看起来更加简洁一点,我们把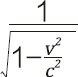 这个时间t前面的系数记为γ(读作伽马),于是可以把这个公式写作:t'=γt,这个γ就是流芳千古的“相对论因子”,也被称为“洛伦兹因子”。你可能奇怪为什么不叫爱因斯坦因子,那是因为荷兰物理学家洛伦兹(Lorentz,1853-1928)首先写出了这个式子,但他没有深刻认识到这个式子的时空含义。洛伦兹是绝对时空观和以太的捍卫者,因此在相对论问世后,洛伦兹与爱因斯坦有过许多争论,不过这并不影响两人建立起深厚的友谊和合作关系。关于洛伦兹的事情我们很快还要提到,这里先放一放,让我们来继续思考时间变慢意味着什么。
这个时间t前面的系数记为γ(读作伽马),于是可以把这个公式写作:t'=γt,这个γ就是流芳千古的“相对论因子”,也被称为“洛伦兹因子”。你可能奇怪为什么不叫爱因斯坦因子,那是因为荷兰物理学家洛伦兹(Lorentz,1853-1928)首先写出了这个式子,但他没有深刻认识到这个式子的时空含义。洛伦兹是绝对时空观和以太的捍卫者,因此在相对论问世后,洛伦兹与爱因斯坦有过许多争论,不过这并不影响两人建立起深厚的友谊和合作关系。关于洛伦兹的事情我们很快还要提到,这里先放一放,让我们来继续思考时间变慢意味着什么。
你可能已经在心底欢呼终于找到了长寿的秘诀,因为运动的速度越快,时间就能变得越慢。姑且认为这没错,那么让我们来粗略地计算一下,你到底能年轻多少呢?先从坐火车开始吧,近似地认为现在火车的速度是200千米/小时,也就是55米/秒,相对论因子γ≈1.000000017。什么意思?也就是说在这列火车上坐了100年以后,你下了车,会发现比你的双胞胎兄弟年轻了53.6秒。火车太废柴了,你暗骂一声,给我换飞机。好,那我们就换飞机吧,飞机的速度大概是300米/秒,γ≈1.0000005,就是说你坐飞机100年以后下来,年轻了26.3分钟。原来飞机也这么废柴,你有点怒了,给我换登月飞船。满足你,我把你换到登月飞船上。登月飞船的速度是10500米/秒,γ≈1.000613063,就是说你在登月飞船上飞100年下来后,年轻了22.4天。这次你可能真的发火了,什么?登月飞船上飞100年也只能年轻22.4天?这叫什么世道啊。给我快、快、快,再快一点!在你的淫威之下,我发明了速度可以达到0.9c的飞船,现在坐上这艘飞船会发生什么呢?相对论因子达到了2.3,也就是说你的衰老速度差不多只相当于地面上人的一半,你的1年等于他们的2.3年,这个γ的神奇之处在于它会随着速度接近光速而迅速增大。
比如我们的速度如果能达到0.99c,则γ≈7,也就是你的1年相当于地球人的7年,如果达到了0.99999c,则γ≈224,你的1年比地球人的两个世纪还长。我们不用再算下去了,因为我知道你已经禁不住开始狂喜了,哈哈哈!原来长生不老真的可以实现啊。对不起,我不得不再次粉碎你的这个长生不老梦。我的计算确实没错,如果你坐上0.99999c的飞船飞了1年后回来,地球确实已经过去了224年之久,但是对于你自己的感受来说,你真真切切的还是只活了1年,一秒钟也不会多,一秒钟也不会少。如果你的寿命是100年,你一直在飞船上飞,当你回到地球的时候,地球确确实实过去了22400年,但是对于你自己来说,仍然只能感受到你自己生命中的100年,一天也没多,一天也没少,每天仍然是24小时,1小时仍然是60分钟。只是在走出飞船舱门的那一刹那,你看见的地球上的景物,已经隔世。你用自己的一生验证了你向前穿梭了22400年的时间。从我们地球人的眼里来看,其实你也并没有比我们潇洒多少,虽然你的1分钟相当于我们的224分钟,可是在我们眼里,你的一切动作全都变慢了,我们吃一个包子1分钟就完了,而在我们眼里,你吃一个包子却要224分钟;我们打一个响指只用1秒钟,而在我们眼里,你却花了224秒钟才慢慢腾腾地把一个响指打完。我们在地球上仰望着飞船中的你,感慨道:“噢,可怜的人啊,行动得比蜗牛还慢,活着还有什么意思呢?”
所以,很遗憾,相对论无法让你长寿。
伽利略的相对性原理这把“倚天剑”,已经被爱因斯坦用他的相对性原理斩为了两截,那伽利略变换呢?伽利略变换此时在你的心中可能也会变得不那么天经地义了,看了前面那些由光速不变推导出来的奇怪结果,你可能已经意识到伽利略变换多半也是站不住脚的。你的想法非常正确,伽利略变换这把“屠龙刀”也早就保不住“武林盟主”的地位了。事实上早在1895年,一位叫作洛伦兹的中年侠士,就已经不把伽利略变换这把“屠龙刀”放在眼里了。
下面,让我来隆重介绍本书最重要的角色之一,来自荷兰的韩德瑞克·安通·洛伦兹先生。各位观众,还记得你们读中学的时候,老师让你们用手握住一个线圈,然后通过大拇指的方向来判断受力方向吗?大声回答我。对了,很好,你们都还记得“左手定则”和“右手定则”吗?什么,你们恨死他了?哦,可以理解,我那个时候也跟你们一样,都快分不清自己的左右手了。电子在磁场中受到的力就是以洛伦兹先生命名的,叫作“洛伦兹力”,什么,我又勾起了你们痛苦的回忆?放轻松,放轻松,我们今天不考试。
洛伦兹在那个年代的物理学界有多出名,有两个事情可以说明。第一件事情,洛伦兹是索尔维会议的定期主席(1911-1927),一直担任到临终前一年。可能你不知道索尔维会议有多牛,那你总知道体育盛会里奥运会最牛,财主盛会里500强财富论坛最牛吧。物理学家的会议里就是索尔维会议最牛了(当然是在20世纪早期)。无图无真相,现在上图:

【图4-8】1927年第五届索尔维会议
这张图片有很多别名,列举一二:物理学全明星梦之队合影、科学史上最珍贵照片、地球上1/3最具智慧的大脑合影。看到没,爱因斯坦居中而坐,他的旁边就是洛伦兹,其他人的名字我就不多说了。无数学校大楼的走廊上、教室里,都挂着这些人的头像,对这些名字你多多少少都会看着眼熟的(你居然还发现了环球快车谋杀案里的三个演员,你或许在想,那艾尔莎应该也有来头吧?哈哈,有的,暂时保密,答案在第六章)。第二件事情,洛伦兹于1928年2月4日在荷兰哈勃姆去世,终年75岁。举行葬礼那天,荷兰全国电信、电话中止三分钟,全世界的科学大师齐聚荷兰,爱因斯坦在他的墓前致悼词。爱因斯坦的悼词中有这样一句话:“洛伦兹先生对我产生了最伟大的影响,他是我们这个时代最伟大、最高尚的人。”
看到此处,相信你对洛伦兹的敬仰已经如滔滔江水了,我也一样。洛伦兹是电磁理论方面的大师级人物,麦克斯韦的电磁方程组在洛伦兹眼里美得不可思议,多少次在梦中都惊叹它的简洁、深刻和美。但是,洛伦兹在研究电子运动的时候,惊讶地发现,伽利略变换和麦克斯韦方程组不可能同时正确,这件事情让洛伦兹非常郁闷,伽利略变换似乎是天经地义的,但是麦克斯韦的方程组更是神圣的。经过一番痛苦的纠结,洛伦兹决定放弃伽利略变换式,麦克斯韦的电磁方程组是神圣不可侵犯的,既然伽利略变换式没法运用到电子的运动上,那什么样的坐标系变换式能呢?洛伦兹用他高超的数学技巧,通过微积分推出了一个变换式,如果用这个坐标变换式取代伽利略的变换式,就和麦克斯韦的电磁方程组不矛盾了。洛伦兹在1904年正式发表了这个著名的变换公式:
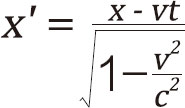
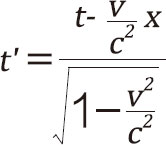
这个式子被人们称为“洛伦兹变换”,在这个式子里面我们看到了熟悉的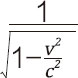 ,这就是为什么把它叫做洛伦兹因子的原因。你可能有点被搞糊涂了,我们前面亲手推导出来的t'和t之间的关系式好像不是这样的嘛?在这里我要提醒我亲爱的读者,你一定要明白坐标变换的概念。所谓坐标变换,就是当你的参照系(不是你自己运动,是你的参照系)在你面前运动的时候,你所处的坐标在运动前和运动到“某一时刻”时所处的新坐标之间的关系。这个关系代表着我们对这个世界中运动和运动之间最本质的认识,换句话说,也就是小红眼中的世界和小明眼中的世界到底有什么不同。所以,洛伦兹变换中的t代表的是“时刻”“时点”,而我们之前那个时间和速度的公式中的t代表的是“时长”“间隔”。这里还要说明的是,在洛伦兹心目中,变换所引入的量仅仅被看作是数学上的辅助手段,并不具有物理本质。
,这就是为什么把它叫做洛伦兹因子的原因。你可能有点被搞糊涂了,我们前面亲手推导出来的t'和t之间的关系式好像不是这样的嘛?在这里我要提醒我亲爱的读者,你一定要明白坐标变换的概念。所谓坐标变换,就是当你的参照系(不是你自己运动,是你的参照系)在你面前运动的时候,你所处的坐标在运动前和运动到“某一时刻”时所处的新坐标之间的关系。这个关系代表着我们对这个世界中运动和运动之间最本质的认识,换句话说,也就是小红眼中的世界和小明眼中的世界到底有什么不同。所以,洛伦兹变换中的t代表的是“时刻”“时点”,而我们之前那个时间和速度的公式中的t代表的是“时长”“间隔”。这里还要说明的是,在洛伦兹心目中,变换所引入的量仅仅被看作是数学上的辅助手段,并不具有物理本质。
洛伦兹可是权威啊!他的这个变换式一经发表,立即引起强烈反响,各界纷纷响应,有赞扬的,有拍马屁的,有质疑的,有惊讶的,当然也有大受启发的(比如当时还默默无闻的小爱同志)。下面是虚构的一场新闻发布会,发布会的主角是洛伦兹,接受全世界同行的提问。请注意这场发布会的时间是1904年,相对论还没有发表,人们对MM实验的结果还在争论不休。
问:“洛伦兹先生,我们注意到您这个新的变换式中含有光速这个参数,很让我们费解,为什么参考系的运动引起的坐标变换,会跟光速c相关呢?”
洛伦兹:“因为电和磁也是运动的一种方式,在考虑它们的运动时,就必然会引出光速这个常数来,至于普通物体的运动为什么会跟光速相关我一下子也说不明白,总之普通物体的运动速度相较光速来说,都小到可以忽略不计,对最终的结果似乎没有什么影响。”
问:“先生,按照您这个公式,一列火车在运动的时候,如果车头取的坐标是x1,车尾的坐标是x2,火车的长度就是x2-x1,根据这个新变换式,我做了一个简单的计算,我发现火车在运动的时候长度居然比静止的时候缩短了,这也有点太不可思议了吧?”
洛伦兹:“根据我的公式,结果确实如你所说,虽然听起来很荒谬,但是我认为这是有可能的,而且有实验可以支持这个现象,就是著名的麦克尔逊-莫雷实验。在这个实验中,我们之所以没有发现干涉条纹的变化,正是因为实验设备在随着地球运动的时候,在运动方向上长度会发生收缩,这个效应刚好抵消了光速的变化。而且根据我的公式计算出来的结果,和实验的结果也吻合得非常好。”
问:“那您依然认为以太是存在的吗?”
洛伦兹:“那当然,以太是一定存在的,我们总会在实验室里把它揪出来的。”
问:“在您的公式中,我还发现一个神奇的地方,时间t'跟速度v和光速c以及坐标x都有关系,坦诚地说,这让我们很费解。难道时间的流逝是不均匀的吗?跟速度相关吗?”
洛伦兹:“千万不要那么想,这只是一种数学的辅助手段而已,时间就是时间,那是上帝主宰的东西,别想打时间的主意。”
问:“您仍然支持牛顿的绝对时空观吗?”
洛伦兹:“当然,毫无疑问。”
新闻发布会在各界的热烈讨论中结束。
洛伦兹变换式发表的时候已经51岁了,人年纪一大,往往就容易失去勇气和丰富的想象力,这导致洛伦兹与伟大的相对论失之交臂。历史有时候真是很有戏剧性,虽然洛伦兹先于爱因斯坦写出了流芳千古的公式,但是,虽曰同工实属异曲,洛伦兹看不穿皇帝的新衣,没有大胆地抛弃以太,也没有大胆地突破牛顿的绝对时空观,在回答时间t'为什么会跟速度相关时,含含糊糊,连自己都说服不了自己。在洛伦兹的脑子里,绝对时空观是神圣不可侵犯的,他一直到死都没有放弃证实以太的存在。一个不可否认的事实是,近100年以来,物理学上取得的几乎所有重大突破,都是杰出的科学家们在30岁左右的时候取得的,量子力学更是被戏称为“男孩物理学”,连爱因斯坦这样伟大的天才,在他人生中的后30年中也没有取得什么重大成就。有一句流传很广的话是这么说的:“如果爱因斯坦在他38岁的时候死了,那么今天这个世界不会有什么不同。”各位亲爱的读者,如果你现在正值20来岁的大好青春年华,请接受我对你的羡慕,你很有可能跨入“男孩”们的行列。
