从专利局办公室窗口跳下去这个想法,的确不是个好创意。他要是说出来,会把同事们吓个半死。前一阵子,物理学界有两位科学家去世了,一位是彼埃尔·居里,他是出门不小心被马车撞死的,居里夫人成了寡妇,这是科学界的意外悲剧。但是另外一件事就更令人惋惜了,统计物理的大牛玻尔兹曼上吊自杀。我们以现在的眼光看来,绝对是抑郁症的结果。玻尔兹曼最大的贡献就是成功地解释了热力学第二定律。热力学第二定律有很多表述,最常见的表述是:“一个封闭系统中,熵只增不减。”熵在统计意义上表示“混乱程度”,熵值越高,混乱度越大。玻尔兹曼自己的大脑熵值抑制不住地增高,直到完全混乱。于是他在度假胜地的宾馆里,用一根窗帘拉绳结束了自己的生命。这样的悲剧也不是孤例,玻尔兹曼的学生埃伦费斯特在1932年也因为抑郁症,用枪打死了自己患有唐氏综合征的小儿子,然后饮弹自尽,想起来就叫人心痛不已。
若是平常开开玩笑,大家也不会当回事,但是有玻尔兹曼的前车之鉴,大家也不敢掉以轻心。爱因斯坦倒是绝没有自杀的意思,毕竟他还有伟大的使命没有完成呢?贝索先生倒是更了解爱因斯坦,他一定想到什么了吧?谁知道呢?反正他脑子里总有奇思妙想。
从楼上跳下去会感受到什么呢?当然是疼啊!然后呢?没有然后了,摔死了嘛!不!爱因斯坦真正注意到的是“失重”,这是至关重要的一个东西。做自由落体的时候,会感到自己失去了重量。在爱因斯坦看来,失重状态就是引力与惯性力完美的抵消了。人在失重状态下,是完全感受不到力的,这岂不就是完美的惯性系?
在传统的观念中,做匀速直线运动的才是惯性系。牛顿的伟大贡献就是指出了地球上的苹果落地和宇宙星辰相互绕行是相同的物理过程。在爱因斯坦看来,一颗炮弹,只要出膛速度是一样的,角度是一样的,无论是一颗铅弹还是一颗石头弹,他们划出的轨迹都是一样的。跟物体材料没有关系,仿佛它们划过的轨迹是空间中固定的轨道一般。
爱因斯坦眼前已经豁然开朗,假如失重状态是完美的惯性系,为什么它走过的路径是曲线而不是直线呢?这显然跟牛顿的描述不相符。因为空间本身是弯曲的,所以惯性运动不见得走直线,在弯曲的空间中,走的就是曲线。爱因斯坦想到了大学的时候,听闵可夫斯基老师讲过的高斯曲面理论。可惜他当时没好好听课,现在看来,真不该逃课。思想上出现了突破,那么现在就可以动手,把相对论推广到更大的适用范围去。

图9-1 等效原理
爱因斯坦提出了非常重要的一个基石,那就是“等效原理”(图9-1)。一个质点,到底是受到引力还是受到惯性力,它根本没法分辨出来。爱因斯坦想象了一个电梯的思想实验,当然我们换用火箭也是一样的道理:一个电梯,静止在地面上,里面“啪哒”掉下个苹果,这是个自由落体运动。在一个匀加速运动的电梯里,你扔一个苹果,那还是一样的结果,也会出现一个自由落体的效果。爱因斯坦说:“这是不能分辨的。”等效原理还分为强等效原理和弱等效原理。弱等效原理就是指,你做力学实验没有办法区分引力和惯性力。强等效原理是指,不仅仅是你做力学实验没法分辨,就算是做电磁学实验,也照样没法分辨,做任何实验都没办法分辨。当然了,爱因斯坦特别强调,这是一点及其邻域的范围内,范围大了,就能分辨了。爱因斯坦的这个惯性系实在是太小了,在一点及其邻域之内是好使的,并不具有实用性,一般还是拿我们地球当做惯性系来对待。当然,太阳参考系是更好的惯性系,银河比太阳又会更好,总之,地面上就是近似惯性系。
经过爱因斯坦的推算,物理学中的时空不再是硬邦邦冷冰冰的概念。时空是柔软的,可以弯曲的,宇宙也是柔软的,可以弯曲的。这就需要一套能在弯曲时空中好用的数学工具,这不是爱因斯坦擅长的领域,即便他当年不逃课,恐怕也搞不定。数学家们总是独自闷在屋里,闷头打造一个又一个稀奇古怪的独门利器。可是他们打造出来以后就往边上一扔,从来也不会去告诉物理学家们。物理学家要到数学家的储藏室里不断地翻找,看看能不能翻出两件趁手的法宝,然而爱因斯坦连去哪儿翻找都不清楚。
在这几年,爱因斯坦并非只考虑引力和惯性的问题,他的职场生涯也已经打开局面,走上了快车道。他先是在专利局升职,年薪已经达到四千五百瑞士法郎,从三等技术专家变成了二等技术专家。他在物理学领域也取得了不少成果:他研究固体比热和黑体辐射,写了好几篇论文,这些论文也普遍得到了大家的认可。爱因斯坦在物理圈子已经小有名气,1908年7月,他接受了日内瓦大学名誉博士学位,9月参加萨尔斯堡德国自然科学家协会第八十一次大会,和普朗克等一班大牛碰了个头,还作了《我们关于辐射的本质和结论的观点的发展》报告。10月份,苏黎世大学聘请他去当副教授,他犹豫不决,因为当教授的工钱不如在专利局多。后来人家特地给他加薪,他才答应从专利局辞职出来,到苏黎世大学任教,这已经是1909年的事了。
1911年2月,洛伦兹请爱因斯坦去荷兰的莱顿大学访问,爱因斯坦就跑了一趟荷兰。后来布拉格大学又要他去当正教授。苏黎世大学着急啊,爱因斯坦不能走啊,我们给你加薪!薪水加到了五千五百瑞士法郎。但是,爱因斯坦还是去了布拉格大学任教。这几所大学都在德语区,不过他到法国能用法语做演讲,跟居里夫人、朗之万也能相谈甚欢。布拉格那时候还在奥匈帝国的统治下,弗兰茨皇帝亲自过问,批准爱因斯坦到布拉格来任教。弗兰茨皇帝当年也是年轻英俊的帅小伙啊,茜茜公主的老公,此时此刻已成为一个八十高龄的老人了。
1911年10月,爱因斯坦去布鲁塞尔出席了索尔维会议,这是当年的物理学家的峰会。工业巨头索尔维因为搞出了大规模的制碱法而发了家,特别想回馈社会。那年头,大富豪们都比赛花钱搞慈善。当然他们搞慈善,并不是直接开粥厂救济穷人,都是投资于人类的未来,文化、艺术、科学技术就成了他们重点关注的对象。卡内基建立了卡内基音乐厅,创办了卡内基梅隆大学,洛克菲勒也在办大学,芝加哥大学就是洛克菲勒办的,后来他还办了洛克菲勒大学。洛克菲勒还广泛投资医学事业,我国的协和医院、协和医科大学就是洛克菲勒家族掏的钱。老头子有一句名言:“把财富带进坟墓是可耻的。”
在这种风气影响下,欧洲人也不甘落后。这个索尔维也想青史留名,搞个科学奖项出来,无奈的是被炸药大王诺贝尔抢先了。人家搞出来个诺贝尔奖,现在成了科学界的最高奖项。索尔维也不甘人后,他打算搞一个顶尖科学家们的定期聚会,为他们提供最好的交流环境,让他们畅所欲言地讨论科学问题。索尔维就找到了一个在科学界有头有脸的人物,他叫能斯特,著名的物理学家、化学家,他最大的贡献是搞清楚了热力学第三定律。热力学第三定律的一种简单的表述就是:“不可能通过有限次操作,把物体的温度降到绝对零度。”他跟工业界和科学界都比较熟,因此就由他出面,邀请了一帮物理学家们,在布鲁塞尔的大都会酒店里面开会,好吃好喝好招待。
能斯特是大会的秘书长,大会主席还是请德高望重的洛伦兹来担任。一直到洛伦兹去世,索尔维会议的主席都是他担任的,他会N国外语,时不时地还要帮着当各国科学家的翻译,万一碰上语言不通的科学家大吵架,洛伦兹老爷子能忙得人仰马翻。有两位年轻的后辈充当大会的秘书,负责整理记录各位大牛的发言。其中一位大会秘书的弟弟后来看到了会议记录,发疯似地爱上了物理学。果然这个小子后来一个雷天下响,因为一篇博士论文而拿到了诺贝尔物理学奖,他姓德布罗意……

图9-2 索尔维会议
现在我们可以看到索尔维会议的照片(图9-2),爱因斯坦在哪儿呢?他在后排最右边第二位,桌子一端坐着的是大会主席洛伦兹。爱因斯坦还是后起之秀,只能往边上站。洛伦兹左边那位就是工业大亨索尔维,不过拍照当天他不在,他的形象是后来用冲洗照片的暗房技术给补上去的,那年头就已经有了类似PS的技术啦。爱因斯坦起码进了大牛们的朋友圈,据说他跟庞加莱聊了聊,后来挺失望,庞加莱不支持他的相对论,恐怕这里面掺杂着感情因素,不完全是对科学的理解问题。庞加莱毕竟离关键的转折点曾经是那么近,哪想到被爱因斯坦这个毛头小伙子抢了先啊!
1912年2月埃伦费斯特来访,爱因斯坦和他一见如故,两个人结成了莫逆之交,爱因斯坦的朋友圈在不断地扩大。10月份,爱因斯坦又回到了母校苏黎世工学院任教。苏黎世工学院1911年已经升格成了有完整博士授予权限的工业大学,格罗斯曼早就留校任教了。爱因斯坦和同窗好友成了同事,因此他才有机会跟格罗斯曼一起研究弯曲时空的问题。格罗斯曼也并不知道该用什么样的办法去计算,他停下自己手头的工作帮爱因斯坦查了好几天的资料,回来告诉爱因斯坦,有几个意大利人正在研究一门学问,叫做黎曼几何,相信这本“武功秘籍”可以帮到你。格罗斯曼是他一生中的贵人,帮了他两次大忙。第一次是大学考试的时候借给他笔记,这样爱因斯坦才能顺利地从大学毕业。第二次是帮助安排了专利局的工作,解决了生计问题。要不然,恐怕也没有这样安逸的环境来保障爱因斯坦的物理学研究。
这一回,是格罗斯曼第三次帮到爱因斯坦。
爱因斯坦早就知道黎曼几何,他当年在奥林匹亚科学院就读过庞加莱的数学科普书籍,知道有黎曼几何这么一门学问。书到用时方恨少啊,这时候爱因斯坦临时抱佛脚去啃黎曼几何,哪有那么好啃!这东西是难以想象的复杂,要了解黎曼几何是怎么回事呢,就必须从几何学的起源讲起。
大家现在普遍都熟悉的几何学,那是古代一个叫做欧几里得的人整理出来的,所以叫做“欧几里得几何学”。当年徐光启碰上了从西方来的传教士利玛窦,俩人谈起《几何原本》这本书,徐光启当时就感到十分惊奇,于是他就缠着利玛窦,俩人一起翻译这本书。为啥徐光启对这本书这么感兴趣呢?因为这是一个用公理系统作为骨架,然后一步步推理出来的逻辑大厦,好几百条的定理,都是由最开始的五条公设推出来的。徐光启知道,我国过去儒家士大夫们对这样的思维方式很不熟悉,古代没有这种东西。这样的思维体系正是西学之精髓所在,正因为有了这种方式,整个数学系统才是一个严密的体系。
欧几里得几何学,是以五条公设开篇的,这五条公设非常重要,它们就是几何学大厦的基石:
1.任意两个点可以通过一条直线连接。
2.任意线段能无限延伸成一条直线。
3.给定任意线段,可以以其一个端点作为圆心,该线段作为半径作一个圆。
4.所有直角都全等。
5.若两条直线都与第三条直线相交,并且在同一边的内角之和小于两个直角,则这两条直线在这一边必定相交。(平行公理)
第五公设说得很复杂,简化版本就是直线外的一点,只能做一条线与此线平行。
这五条公设人为设定,是显而易见不证自明的。欧几里得的设定都是日常司空见惯的东西,是长期的实践中检验过的,因此整个欧几里得几何学与实际的生产生活之中的测量结果完全符合。
但是大家觉得有点不爽的是第五公设,也就是平行公设。前面几条都简单易懂,一句话解决问题,但是这个第五公设就描述得十分啰唆,而且,欧几里得的前二十九项都没用到第五公设。大家想,第五公设能不能简化呢?又或者能不能去掉这条公设,从其他的公设推出这一条?要知道,一个体系的公设越少,那么普适性就越好。到了十九世纪,好多数学家就跟这条公设不断地死磕。
一般来讲,这种极端基础的问题,直接证明是很困难的。大家就想到了反证法,能推出矛盾,就说明假设是错误的,那也就反证了第五公设是对的。首先是意大利的数学家萨开里设想了一个萨开里四边形(图9-3)。一共四个角,两个底角是直角,剩下的两个角呢?他假设三种情况:
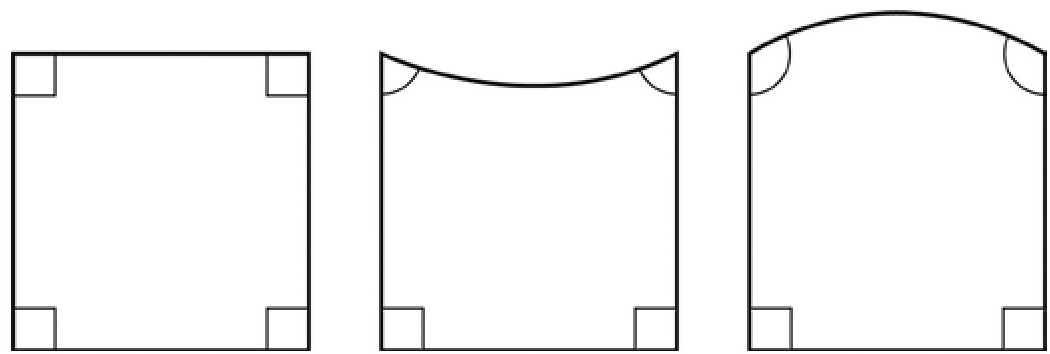
图9-3 萨开里四边形
1.都是直角,那么与跟欧几里得一致。
2.都是锐角?
3.都是钝角?
假如锐角成立呢?看看有啥奇葩的结论出来,他一口气推导了三十几个定理,这些定理都很古怪。萨开里觉得,差不多了,这些奇葩的结论肯定不靠谱啊,那么第五公设应该是没问题的。
后来出场的是个匈牙利人,他叫亚诺什·鲍耶,他也跟这平行公设过不去,也死磕第五公设。他的父亲是著名数学家法尔科斯·鲍耶,老爹一看儿子跟第五公设死磕,当时连哭的心都有了,自己当年也曾希望把几何学中的这个白璧“微瑕”消除干净,但发现最后只是赔上了自己的时间、健康和生活的快乐。亚诺什倒是觉得,虽然推导出来的结论很古怪,但并非真的有矛盾,这种几何学,看着虽然不爽,看时间长了,慢慢也就习惯了。那时候,一批数学家就开始鼓捣这种偏离了欧几里得祖师爷的几何学,统称叫做“非欧几何”。
1832年亚诺什的论文最后还是作为他父亲用拉丁文所写的数学书的附录发表了,老爹到底是向着儿子。法尔科斯还写信给了大数学家高斯寻求帮助,高斯号称数学王子,各个方面都有涉及,是哥廷根数学学派的开山祖师爷。高斯自己也有类似的想法,十五岁的时候,他也和第五公设死磕过一阵子,这种想法大家都曾经有过。高斯接触非欧几何也不是平白无故地找祖师爷欧几里得麻烦,而在大地测量学之中常常碰到弯曲表面的形状计算。大地表面毕竟是个球面,并非是平面。
于是高斯写了封回信,信里写道:“如果我一上来就说我不能赞赏这项工作,你一定会大吃一惊,但我不得不这么说,因为赞赏这篇附录就等于赞赏我自己。实际上这篇附录的方法和结果,都和我三十年来的某些工作极其类似……我认为你的儿子有着第一流的天赋。”老爹法尔科斯一看回信,心里还是蛮高兴的,毕竟儿子和大名鼎鼎的高斯想到一起去了!可儿子亚诺什却憋了一肚子气,自己辛辛苦苦地折腾半天,高斯就来了这么一句评语,这简直是“还乡团下山摘桃子”啊!你让他怎么能舒心呢?亚诺什心眼有点小,后来发现罗巴切夫斯基拿出的东西跟自己的很相似,第一反应还是认为人家是剽窃。后来才搞清楚,人家完全是独立思考的结果,之后他还是蛮支持罗巴切夫斯基的。
高斯当然了解非欧几何研究的一些动态,但是他主要还是把精力放在了微分几何上。这是一门运用微积分来研究空间的几何性质的数学学科,高斯就是微分几何的开创者,他还跟俄国的罗巴切夫斯基通了信。这个罗巴切夫斯基是俄罗斯喀山大学毕业的,然后就留校任教了。他们之间也讨论了不少有关第五公设的事,最后就是这个罗巴切夫斯基把这个工作给完成了。
罗巴切夫斯基设定:过已知直线外一点至少可以作两条直线与已知直线平行,代替欧几里得的第五公设。在这个前提下,他推导出了一整套几何学。他也认为,这些理论非常古怪,但是系统内部是没有矛盾的。1826年,他发表了论文,那时候他还是个年轻人,站上讲台宣讲他的理论,底下的一大群教授听他讲得云山雾罩,脑洞大开,一个个都冷嘲热讽的,还有人直接就写文章骂他。他写了篇回应的文章,但是人家杂志社审核没通过,硬是没给发表。然而罗巴切夫斯基顶住了压力,他坚信自己是正确的。不仅数学家冷嘲热讽,连文学家也来凑热闹,德国的歌德在《浮士德》中写道:“有几何兮,名为非欧,自己嘲笑,莫名其妙。”高斯是罗巴切夫斯基的朋友,私下里挑大拇指称赞罗巴切夫斯基了不起啊,但是在公开场合,高斯一句鼓励的话也没说。罗巴切夫斯基后来当了喀山大学的校长,去世的时候大家都说了一堆冠冕堂皇的话,他给喀山大学做了多少多少贡献等等,但是对他的几何学,一个字都没提。
罗巴切夫斯基的这一套几何学与欧几里得的几何学是不一样的,因此也被称为“罗氏几何”。他去世的时候是景况凄凉,死后不久,意大利的数学家贝特拉米就证明了,其实罗氏几何学是在弯曲的表面上实现的几何学。欧式几何与罗氏几何这两个看似矛盾的理论体系,其实并不矛盾,彼此之间是可以互相转换的。如果欧几里得的几何学是正确的,那么罗巴切夫斯基的几何学也是正确的。人们这才豁然开朗,罗巴切夫斯基也被称为数学界的哥白尼。因为他打破了欧几里得几何学的一统天下,大大扩展了数学界的视野。原来早已经熟悉的几何学还能这么玩儿啊!到了1893年,喀山大学的门口为他树立了一座雕像,纪念他在几何学上的成就,这也是第一次为数学家塑像。当然啦,喀山大学的人物像不止一座,有一座雕像,雕刻的是一个年轻人,他背着行囊,风尘仆仆的样子,仿佛要去远方旅行。这个年轻人叫弗拉基米尔·伊里奇·乌里扬诺夫,他自己也不喜欢这个贵族化的名字,另外一个名字震撼了整个二十世纪,他的笔名叫列宁。
罗巴切夫斯基的假设是过直线外一点,起码可以做出两条线与此直线平行。有人就开始唱反调了:别说两条平行线,一条都做不出来,不存在平行这种情况,必定是要相交的。敢出此狂言的人是谁啊?此人叫黎曼,他是高斯的学生,也推出了一整套几何学,叫“黎曼几何”。要知道,杨振宁点出了几个在几何学的发展史上做出重大贡献的人物,那就是所谓的“欧高黎嘉陈”:欧几里得、高斯、黎曼、嘉当、陈省身。这个黎曼可不得了,能够成为几何学大家,功力非同小可。他描述的是球面的状况,罗巴切夫斯基描述的是马鞍面的状况,欧几里得描述的是平面的状况。各种稀奇古怪的几何学,本质上其实就是空间弯曲方式不一样造成的。黎曼延续的是老师高斯的微分几何的思想,空间弯成什么样子都能计算。
在弯曲的空间里,是没有直线可言的,只有在欧几里得空间中才会有真正意义上的直线,弯曲空间中只有“短程线”这个概念。我们用地球表面做例子:地球是个球面,从上海飞往洛杉矶的飞机航线,往往要路过日本和阿留申群岛。我们在地图上看,并不是简单地沿着纬线在走,而是沿着“大圆航线”在飞行。航空公司当然愿意把油水榨干,没人愿意走费力不讨好的长线。地球上两点间路程最短的线,顾名思义叫“短程线”,也叫“大圆航线”。南北极之间有无数条短程线,经线都是短程线,但是上海到洛杉矶之间,只有一条短程线。
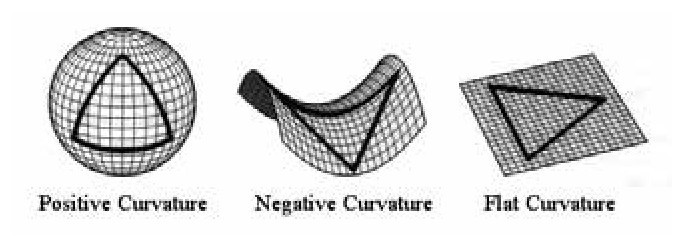
图9-4 弯曲空间里的三角形
球面上的三角形,内角和总是大于180度的。双曲面上的三角形,内角和总是小于180度。平面上上的三角形,恰好等于180度。(图9-4)
短程线在大地测量学上很常用,因此还有另外一个名称叫做“测地线”。广义相对论中也借用了这个概念。不过奇葩的是,测地线在广义相对论里,反而是两点间最长的线,并非最短。还记得我们前面讲述“双生子佯谬”时提到过的闵可夫斯基时空吗?时间轴是“虚数”。前面那个负号导致了一系列奇葩的结论,曲线反而比直线短。在广义相对论中,也还是类似的情况:弯曲的四维时空中,测地线是最长的线。这样古怪的几何学,没多少人懂也是常理。
就在黎曼和许多数学家的推动下,非欧几里得几何学得到非常大的发展。高斯自己也推导过曲面理论,他生前没有发表过这方面的著作,很多思想都记录在与朋友们的通信中。他开创的微分几何思想正是解决弯曲空间的重要途径,但是他只推导了三维空间内的情况,对于四维空间甚至是高维空间应该是什么样的,他并没有涉及。他的学生黎曼在这方面走得比老师可远多了,他按照高斯的微分几何思想来建立自己的体系,空间不管如何弯曲,在一个微小的局部总是可以建立一个类似欧几里得平直空间的坐标系统,广义相对论的计算全都离不开这种微分几何的思想。
格罗斯曼和爱因斯坦,在数学资料里面一顿找,最后他们发现,黎曼的几何理论最合适。他们需要处理的那些恼人的问题:黎曼、里奇和勒维他们已经解决了,爱因斯坦和格罗斯曼正式把黎曼几何引入相对论的研究中。一百多年前,拉格朗日、拉普拉斯他们几个法国人用漂亮的微分方程把牛顿喜爱的几何方法扫地出门,哪知道几何学竟然以如此玄妙的方式高调回归了物理学界,二十世纪的物理学革命,很大程度上得益于数学工具的发展。理论物理领域,数学早就与物理水乳交融不可分离。
爱因斯坦尽管找到了称手的数学工具,但是在探索广义相对论的道路上仍然是屡屡碰壁。因为数学提供了太多的可能性,到底哪一条路才是正确的呢?爱因斯坦不得不花费极大的精力去一一尝试。他探索广义相对论的历程曲折而漫长,从1907年他开始有初步的打算,一直到他最终拿出完整好用的理论,花了近八年时间。因此,广义相对论并不是像狭义相对论那样,“砰”地一声就搞定了。狭义相对论最大的难度是在观念的突破上,广义相对论则要难得多。爱因斯坦和格罗斯曼引入了一个比较陌生的概念,叫做“张量分析”。“张量”这个概念很难通俗地解释清楚,大约可以描述一下:标量是0阶张量,1阶张量就是矢量。普通人都是一个头两个大,但是张量分析是广义相对论必须使用的手段,躲也躲不开。
广义相对论的推导过程是个漫长的历程,当时爱因斯坦已经在物理学界小有名气,还参加了索尔维会议,因此社会活动也越来越多。他受邀去法国访问,见到了朗之万和居里夫人,还用法语演讲,几个人聊得都挺投机。爱因斯坦跟朗之万聊了聊,话题当然离不开引力问题。爱因斯坦邀请他们来阿里苏黎世访问,后来,法国人还真的到苏黎世访问了爱因斯坦。大家讨论的主要议题集中在原子模型上,当时有个年轻人提出了一个新的原子结构模型。爱因斯坦当时大概不会想到,他和这个年轻人保持了一辈子的友谊,也吵了一辈子的架。这个年轻人叫玻尔。
1913年7月,能斯特和普朗克跑到苏黎世拜访爱因斯坦。普朗克和能斯特来访,苏黎世都有点儿受宠若惊的样子。大家纷纷传诵:能让能斯特亲自跑一趟的这个家伙,一定是不得了的大人物。这回不但是能斯特来了,普朗克也来了,无事不登三宝殿,这二位来到苏黎世所为何故呢?他俩来请贤啊!邀请爱因斯坦到德国去入伙:“德国这个山头大,你来入伙吧!”两位世界级顶尖科学家组成的猎头团队是有史以来最强的!其实爱因斯坦并不喜欢德国,如果他喜欢德国,何苦中学时代就放弃了德国国籍呢?可如今到德国工作,是威廉二世皇帝特批的,皇帝陛下的面子也不能不给啊!爱因斯坦经不住这两位前辈一顿劝,答应了回故乡德国发展。当然爱因斯坦还有一堆事务要处理,并不是马上就能动身的。
就在1913年底,爱因斯坦和格罗斯曼一起发表了一篇论文——《广义相对论和引力理论纲要》。数学部分格罗斯曼操刀,物理部分是爱因斯坦的手笔。这篇论文中首先提到了引力场方程,黎曼几何第一次有了实实在在的物理学意义,不再是数学家们脑子里的奇妙空想。但是这方程仅仅是一个初步的成果,还有许多毛病要去解决,爱因斯坦为了解决这些毛病又足足花了两年的时间。在此期间,他给美国威尔逊山天文台的台长海耳写了一封信,差点让海耳台长把他当成无知的疯子。他问了一个普通人都不会问的问题,那就是——白天能看见星星吗?
