正如我们在第5章看到的,任何一个具有有效形式的论证本身也是有效的,可以看作这个形式的替换例或事例。任何一个无效形式的代入例本身也是无效的。然而,命题逻辑系统具有大量的无效或有效形式。因此,仅仅通过辨识某一论证是一个有效式或无效式的例示是不可能学到命题逻辑系统中论证的有效性或无效性知识的。但能够辨识一些最常见的有效式或无效式也是非常有益的。我们将重新考察第5章已经介绍过的五种形式,学习如何认出例示那些形式的论证。
肯定前件式
肯定前件式是一种常见有效式,它的一个前提是条件句,另一个前提是条件句前件的肯定,结论是后件的肯定。如,
例12-10 1. 如果乔斯是消防员,那么他就为消防队工作。
2. 乔斯是消防员。
3. 乔斯是为消防队工作。
这个论证举例说明了“肯定前件式”(字面意义是“肯定的模式”)这一有效式,其符号表示是,
例12-10a 1. P∩Q
2. P
3. Q
因为实质条件句的前件表达的是后件的充分条件,前件在肯定前件式中被断定为真,任何具有这一形式的论证都有效。换句话说,如果P蕴涵Q为真,并且P为真,那么Q必然为真。具有这一形式的论证的有效性可以通过真值表例12-11证明。
例12-11
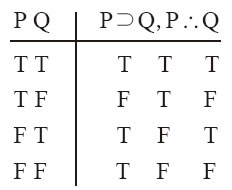
可以看出,这个真值表中并没有两个前提都真,但结论为假的行。
否定后件式
另一常见的有效形式是否定后件式(字面意思是“否定的模式”)。如果一个论证包含两个前提,一个是条件句,另一个是对条件句后件的否定,那么这个论证就是否定后件式的代入例。结论是对条件前提的前件的否定。如,
例12-12 1. 如果铜是一种稀有金属,那么就很昂贵。
2. 铜并不昂贵。
3. 铜不是稀有金属。
这个论证的形式是否定后件式,可表示如下:
例12-12a 1. P∩Q
2.~Q
3.~P
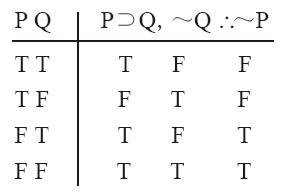
实质条件句中,后件表达的是前件的必要条件。如果Q对P是必要的,那么若非Q,则非P。换句话说,否定一个前提的后件可以推出否定其前件。如下表表明,任何否定后件式的代入例都是有效的:
例12-13
换质位
换质位论证的前提是一个单称的条件句,结论不仅交换了条件句前后件的位置,而且改变了前后件的质,这个论证具有的就是换质位形式。如,
例12-14 1. 如果安娜是一名革命者,那么她就反对建立秩序。
2. 如果安娜不反对建立秩序,那么她就不是一名革命者。
例12-14的形式正是换质位,因为:
例12-14a 1.P∩Q
2.~Q∩~P
例12-14a使我们认识到,因为例12-14的形式有效,所以论证本身也是有效的。为什么有效?与否定后件式类似:因为Q是实质条件句的后件,是其前件P的必要条件。因此,如果Q假,P一定假。换质位的有效性可由下列真值表表明:
例12-15
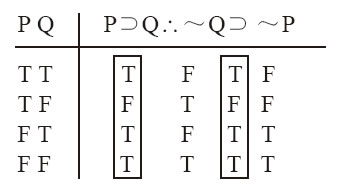
假言三段论
之所以称假言三段论,是因为这种论证有两个前提(与三段论相同),而且其前提(和结论)都是假言或条件命题。如:
例12-16 1. 如果伊莱恩是新闻报道者,那么她就是记者。
2. 如果她是记者,那么她就知道如何写作。
3. 如果伊莱恩是新闻报道者,那么她就知道如何写作。
其形式如下:
例12-16a 1. P∩Q
2. Q∩R
3. P∩R
例12-16a使我们明白,例12-16具有假言三段论这一有效形式。
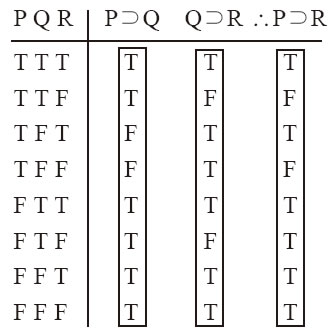
仔细考察这个形式就会发现前提1的后件是前提2的前件,而前提1的前件与前提2的后件分别是结论的前件和后件。显然,因为条件命题的前件表达的是后件的充分条件,Q又是P的充分条件,这可以推出P是R的充分条件。例12-16是这个形式的代入例,因此是有效的。下列真值表可以表明假言三段论的有效性:
例12-17
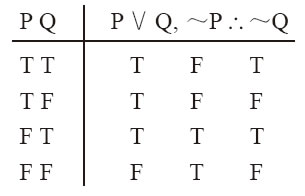
析取三段论
最后,我们要讨论一种不涉及条件前提的有效论证形式:析取三段论。之所以称析取三段论,是因为它有两个前提(与三段论相同),并且其中一个是析取式。一个前提表达的是析取式,另一个是对析取式的一个析取支的否定,这可以导出结论是另一个析取支的肯定。如:
例12-18 1. 我的汽车要么是被警察拖走了,要么是被偷了。
2. 我的汽车并没有被警察拖走。
3. 我的汽车是被偷走了。
例12-18是析取三段论的一个代入例。由于否定的析取支不同,析取三段论又可以分为以下两种形式,它们之一可以精确地刻画例12-18:
例12-18a 1. P∨Q 例12-18b 1. P∨Q 2. ~P2. ~Q 3. Q 3. P因为例12-18否定的是析取前提的第一个析取支,所以正确形式应是例12-18a。但无论是哪种形式,根本原则是:已知相容析取的真值函项定义,如果相容析取前提为真,但其中一个析取支为假,就可以推出另一个析取支为真。因此,正如下列真值表可以证明,任意具有例12-18a或例12-18b形式的论证都有效:
例12-19
更复杂的有效代入例
当着手分析命题逻辑系统中的论证时,能够辨识上述五种基本的有效形式将是非常有益的。只要某个论证具有上述形式之一,它就有效,不需要进一步的程序!一个论证有效,只要其前提和结论所反映的形式有效即可。这就意味着一个有效论证的前提和结论除主要反映有效形式中的前提和结论之外,还在描述联结词方面起到了十分重要的作用。只要形式和论证的主联结词完全相同就没有问题。以下是我们在判定某一论证具有何种形式时需要识记的几点内容:
(1)一个具体论证,其前提的顺序与它本身是否具有肯定前件、否定后件、假言三段论或析取三段论形式这一问题无关。
(2)联结词除标准的表述之外,还有其他表述方式。
(3)双重否定可以消去。因此,任何不包含否定的命题都可以解释为具有双重否定的命题。
(4)一个有效论证除与基本的有效形式中的主联结词对应之外,还要与形式中的其他部分对应。
下列论证可以说明(1)和(3):
例12-20 如果跳蚤是微生物,那么就是裸眼不可见的。但跳蚤是裸眼可见的,因此,它们不是微生物。
例12-20这个论证是否定后件式的代入例:
例12-20a 1. E
2. M∩~E
3.~M
依据(3),前提1中的E等价于~~E,即2的后件──~E的否定。而结论3是对前件的否定。依据(1),这正是否定后件式!
以下论证可以例证(2):
例12-21 1. 只有空袭结束,军舰才可以起航。
2. 空袭没有结束。
3. 军舰不能起航。
一旦使用“如果……那么”这样的标准形式替换“只有……才”,那么例12-21显然是否定后件式的代入例,论证形式是:
例12-21a 1. C∩O
2.~O
3.~C
为什么例12-21的第一个前提可以表示为H∩L的形式?因为“只有……才”是条件句的另一种日常语言表达方式。例12-21中,条件句的前件是“只有”命题之后的命题,后件就是“只有”命题。回顾第11章所讲的复合命题,温习真值函项联结词不同表达方式的知识。但是,还有另一个与(1)相关的例子,这次是用“除非”而不是“或者”表达析取。一旦知道什么词与“除非”等价,就能辨识例12-22、这个析取三段论的形式是例12-22a:
例12-22 1. 乔治今晚会看《辛普森一家》,除非他去踢球。
2. 他今晚不踢足球。
3. 乔治今晚会看《辛普森一家》。
例12-22a 1. G∨F
2.~F
3. G
与上述(1)和(3)相关的另一个例子如下:
例12-23 1. 艾迪是银行雇员蕴涵他有工作。
2. 艾迪只有是银行雇员,才可以是银行支票员。
3. 艾迪是一名银行支票员蕴涵他有工作。
前提的顺序(上例是倒置)以及“蕴涵”和“只有……才”,都不妨碍把例12-23看作假言三段论的一个代入例。一旦我们按照逻辑顺序排列前提,使用形如例12-23a中的符号语言表示上述论证。如例12-23所示,令E表示“艾迪是银行雇员”,B表示“艾迪是银行支票员”,J表示“艾迪有工作”,一旦我们依照逻辑顺序重新排列前提,并把例12-23翻译成符号语言,前述观点就是显然的。
例12-23a 1. E∩B
2. B∩J
3. E∩J
现在,考察以下论证以及它们的形式表征:
例12-24 1. 哥斯达黎加是一个和平的国家,而且这个国家没有军队。
2. 哥斯达黎加只有没有公众骚乱,才是一个和平并且没有军队的国家。
3. 哥斯达黎加没有公众骚乱。
例12-24a 1. C ·∨~A
2.(C·~A)∩~N
3.~N
例12-25 1. 乔伊要么在欧洲受审,要么被引渡美国。
2. 乔伊要么在欧洲受审,要么被引渡美国,蕴涵他辩护失败而且不是自由身。
3. 乔伊辩护失败而且不是自由身。
例12-25a 1. J∨E
2.(J∨E)∩(D ·~F)
3. D ·~F
严格地从前提与结论之间的主联结词的角度看,上述两个论证都是肯定前件式的代入例。因为两个论证都由一个条件前提(恰好是第二个前提)以及条件前提前件的肯定(恰好是第一个前提)构成。一个论证中,前提的排列顺序以及前提本身是包含若干联结词的复合命题,这两点都不会影响整个论证成为肯定前件式的代入例。
一些标准的无效论证形式
我们已经看到,有很多种缺陷可以导致论证不成立。不同缺陷构成了所谓的谬误,包括已经讨论过的非形式谬误。现在,我们来讨论它们在命题逻辑系统中的表现形式,包括一些形式谬误。(如图12-1所示)
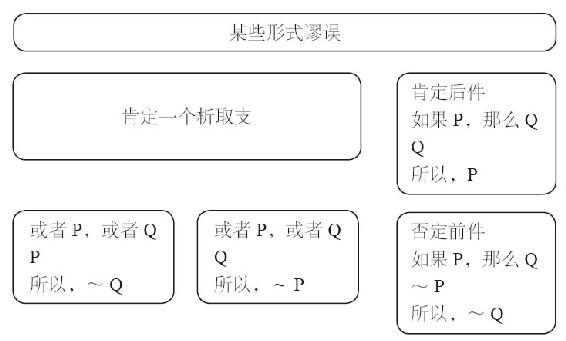
图12-1 无效的论证形式
所有形式谬误都与有效式非常类似,但又有某种程度上的区别。因此,它们是无效的演绎论证形式的代入例。一个论证是无效的,当且仅当具有这一形式的论证有可能前提真而结论假。为了证明一个论证形式的无效性,只需找到一个具有相同形式的论证具有真前提和假结论。如:
例12-26 1. 如果信使来了,钟会在中午响起。
2. 钟在中午响起。
3. 信使来了。
这个论证是无效的,因为其前提为真、结论为假是可能的。即使在有些例子中,前提和结论在某种情形下都是真的,也会存在其他情形。其中,具有相同形式的论证可能具有真前提和假结论。
假设信使没来,但钟确实在中午响了,尽管钟是被邻居敲响的。此时,例12-26的前提都为真,但结论为假。因此,当前这个情形就等价于可以显示例12-26无效的反例。
通常在现实生活中,我们都会找到一个反例证明特定论证的无效性。但我们也可以不用反例,因为说明一个论证无效,只需描述一个“可能世界”(可以是、也可以不是现实世界──仅仅是一个内部没有矛盾的情境)。其中,具有相同形式的论证可能具有真前提和假结论。
因此,一个论证的无效性可以通过上述方式证明:试图描述一个可能情境,其中,当前讨论的论证前提真、结论假。如果提不出这样的情境,可以先抽象出论证形式。例12-26的形式如下:
例12-26a 1. P∩Q
2. Q
3. P
然后找到一个具有相同形式的论证,在某一可能情形中前提为真,结论为假。如,
例12-27 1. 如果贝拉克·奥巴马是共和党,那么他就是一个政党的成员。
2. 他是一个政党的成员。
3. 贝拉克·奥巴马是共和党。
例12-27表明在现实世界,一个具有相同形式的论证(如例12-27)具有真前提和假结论。依据无效的定义,例12-27无效。它等价于任何具有相同形式论证的反例。
肯定后件
上述无效论证都是肯定后件式的代入例。
肯定后件谬误是指一个论证具有一个条件句前提,另一个前提肯定了条件句的后件,其结论是对条件句前件的肯定。
肯定一个命题就等于说它为真。犯了这一谬误的论证所肯定的是一个实质条件句的后件。后件总是表达前件的必要而非充分条件。所以,后件的真绝不能确保前件(结论)的真。以下是一个较复杂的肯定后件的示例:
例12-28 1. 如果奥尔森一家是猎鹿者,那么,若他们打猎,则不打野鸡。
2. 若奥尔森一家打猎,则不打野鸡。
3. 奥尔森一家是猎鹿者。
例12-28a 1. O∩(H∩~A)
2. H∩~A
3. O
与任何肯定后件式的代入例相同,例12-28也是无效的。这一形式的无效性可通过如下真值表说明:
例12-29
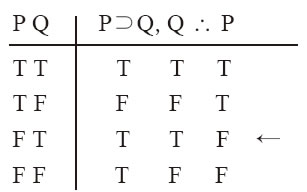
正如你能看到,这个真值表中有一行是前提都真,但结论为假。
专栏12-3 如何避免肯定后件式谬误
在肯定前件式中,一个前提肯定的是另一个前提的前件(而不是后件),同时结论肯定的是其后件。
因此,要谨慎对待看起来像但实际上不是肯定前件式的论证,因为其条件前提的后件被另一个前提所肯定(而它的后件由结论肯定)。
否定前件式
另一个形式谬误是否定前件式。
否定前件式是这样一种谬误,其中一个前提是条件形式,另一个前提是条件前提前件的否定,结论是条件前提后件的否定。
假设我们遇到了如下论证:
例12-30 1. 如果奥斯卡是波士顿交响乐团的提琴手,那么他就懂乐谱。
2. 事实上,奥斯卡并不是波士顿交响乐团的提琴手。
3. 他不懂乐谱。
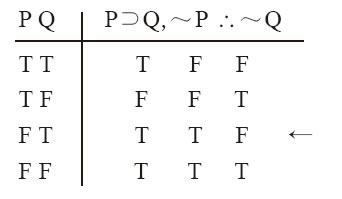
显然,这个论证无效。“奥斯卡是波士顿交响乐管弦乐队的提琴手”是“懂乐谱”的充分条件(如果他在该乐团,那么就懂乐谱)。但不是必要条件,因为有很多不在该乐团中的人都懂乐谱。因此,“他不懂乐谱”不能被必然地推出。简而言之,例12-30无效,因为它犯了否定前件谬误。更普通地说,任何例示这一谬误的论证都是无效的,因为否定条件前提的前件等于说前件假。但实质条件句的前件表达的是后件的充分条件:所以前件假,结论可能是真的。因此,否定条件句的前件不能推出后件的否定。上述论证就是否定前件式的代入例。任何犯了这类谬误的论证都具有以下形式:
例12-30a 1. P∩Q
2.~P
3.~Q
否定后件的无效性可通过真值表例12-31得到说明:
例12-31
专栏12-4 如何避免否定前件式谬误
在否定后件式中,条件前提的后件被另一个前提否定(结论正是对前件的否定)。
因此,谨慎对待看起来像但实际上不是否定后件式的论证,因为其条件前提的前件被另一个前提所否定(同时论证的结论是后件的否定)。
肯定一个析取支
另一个形式谬误是“肯定一个析取支”。
犯“肯定一个析取支”谬误的论证,特征是其中一个前提是相容析取,另一个前提肯定了前者的一个析取支,结论是对另一个析取支的否定。
肯定一个析取支是无效形式,则是因为,我们是在相容意义上(即,P或者Q,或P并且Q)理解“或者”的。除两个析取支都为假外,相容析取在其他情况下都是真的。因此,假设一个相容析取为真,否定其中一个析取支(即说它为假),可以推出另一个析取支一定为真。但肯定一个析取支(说它为真)并不能推出另一个析取支的否定,即不能推出另一个析取支为假。(在不相容析取的情况下,“肯定一个析取支”并不是谬误)如:
例12-32 1. 我的汽车或者被警察拖走了,或者被偷了。
2. 事实上,我的汽车被警察拖走了。
3. 我的汽车没被偷走。
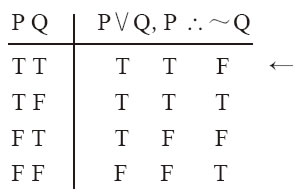
两个前提都为真的情况下,上述结论有可能为假吗?有可能!一种可能情况是,盗窃犯在晚上撬开了汽车,然后非法停车,因此被警察拖走。如果是这种情况,例12-32的前提就都是真的,但结论为假。因此,结论并不必然地从前提推出──也是推不出的。因此,论证无效。任何具有下述一种形式的论证都会犯这样的谬误:
例12-32a
Ⅰ1. P∨QⅡ1. P∨Q 2. P2. Q 3.~Q3.~P因为例12-32中的“或者……或者……”是相容析取,肯定其中一个选言支并不能推出否定另一个。从相容析取的角度看,上述两种形式都无效。肯定一个析取支的无效性可通过下列真值表说明:
例12-33
现在已经识别出了与三种形式谬误对应的无效论证形式。如果一个论证具有上述形式之一,那么并不需要通过真值表判定它是否有效。仅需指出这个论证具有:肯定后件、否定前件或肯定一个析取支的形式即可。如果你能区分这三种无效式和之前讨论的五种有效式,那么就会比较容易地区分无效论证和有效论证。
专栏12-5 如何避免“肯定一个析取支”谬误
注意,析取三段论的前提否定的是另一个前提的析取支,结论肯定的是另一个析取支。
因此,要谨慎对待看起来像但实际上不是析取三段论的论证,因为其前提肯定的是另一个前提的析取支,而结论否定的是剩下的析取支。
一种证明有效性的简明方法
上文讨论的一些有效论证形式通常被用作有效性证明中的基本推理规则。这是一种程序,旨在展示一个命题逻辑有效论证的结论是如何从其前提一步一步推导出来的。假设一个论证事实上是有效的,可以通过建构一个证明显示这一点。在准备构造这类证明之前,我们将补充一些基本的有效形式和替换规则,使我们拥有足够多的证明所需要的推理规则。
基本原则
为了建构有效性证明,我们需要一些有效论证形式以及一些复合命题之间的等价关系。前者可以作为推理规则,使我们从一个前提或多个前提推出结论。后者可以作为替换原则,允许我们使用一个表达式替换另一个与之等价的表达式。我们的规则可表示如下:
基本的推理规则
(1)肯定前件式(MP)P∩Q,P∴Q (2)否定后件式(MT)P∩Q,~Q∴~P (3)假言三段论(HS)P∩Q,Q∩R∴P∩R (4)析取三段论(DS)P∨Q,~P∴Q (5)简化律(Simp)P · Q,∴P (6)合取律(Conj)P,Q∴P · Q (7)附加律(Add)P∴P∨Q基本的替换规则
(8)换质位(Contr)(P∩Q)≡(~Q∩~P) (9)双重否定(DN)P≡~~P (10)德摩根律(DeM)~(P · Q)≡~P∨~Q ~(P∨Q)≡~P ·~Q (11)交换律 (Com)(P∨Q)≡(Q∨P) (P · Q)≡(Q · P) 12)实质条件的定义(Cond)( (P∩Q)≡(~P∨Q) (13)是指等价的定义(Bicond)(P≡Q)≡[(P∩Q)·(Q∩P)] (P≡Q)≡[(P · Q) ·(~P∩~Q)]什么是有效性证明
有效性证明可以是形式的,也可以是非形式的。在一个形式化的有效性证明中,推出关系是指在一个逻辑系统内部严格获得的某些合式公式之间的关系,这些公式不必具有一个自然语言(英语、葡萄牙语或普通话)解释。而且,形式证明所使用的基本推理和替换规则可以证明任意从命题逻辑有效论证的前提推出的结论。另一方面,非形式证明中的推出关系是自然语言可表达的特定命题之间的关系。如果推出的证明仅涉及公式,那么可以假设在那些公式中有一个自然语言的解释。另外,使用非形式方法的基本规则不能为所有命题逻辑有效的论证提供一个有效性证明。
尽管我们为了方便,在构造一些论证的有效性证明时使用的是符号语言,但可以假设那些论证都有一个自然语言解释。对于自然语言表达的有效论证,首先把它翻译为符号语言。然后使用上述规则证明它们的有效性。这些规则可以用于证明许多论证的命题逻辑有效性,下文将会讨论如何使用规则证明有效性。
无论形式方法还是非形式方法,所有有效性证明都要求在对前提使用一个或多个推理和替换规则之后,原则上是可以推出结论的。这些规则被公认是“基本”的。(因为这个系统内的任何证明都至少需要预设几个基本的、在本系统内不能证明的规则)
如何构造一个有效性证明
现在使用上述基本规则证明下列论证的有效性:
例12-34 爱丽丝和卡洛琳将都在明年毕业。但如果卡洛琳明年毕业,那么吉赛尔就会获得奖学金,当且仅当爱丽丝明年毕业。因此,要么吉赛尔会获得奖学金,当且仅当爱丽丝明年毕业,要么海伦会是致告别辞的优秀毕业生。
首先把这个论证翻译为如下符号语言:
例12-34a A · C,C∩(G≡A)∴(G≡A)∨H
现在可以证明这个论证的结论,(G≡A)∨H可从前提推出。如何证明?仅对例12-34a的前提应用基本的推理和替换规则。从例12-34a的前提演绎出结论的四个步骤(3、4、5、6)分别是:
例12-34b
1. A · C 2. C∩(G≡A)∴(G≡A)∨H 3. C·A1──交换律 4. C3──简化律 5. G≡A2、4──肯前式 6.(G≡A)∨H5──附加律第3行是对前提1使用交换律(参看上述交换律规则),从而演绎出C · A。每演绎出一个公式,都要在右边注明依据。如这个例子,表达依据的语词包括“从”、“且”、“通过”,下文将省略(从)或使用标点替换(“且”和“通过”)。书写依据时要注意两点:(1)标明应用特定规则的前提序号(若多于一个,则按顺序写);(2)阐明所用到的规则名称。如果证明了某一公式,那么可以把它看作新前提,标明序号。因为第3行的C · A已经从论证的前提演绎出来了,那么就可以用于进一步证明的前提。事实上,它在第4行被用作导出C的依据。第5行,前提2和4通过肯前式导出了G≡A。第6行,使用附加律导出了结论,从而证明了例12-34的有效性。如此,例12-34的有效性得证。
证明和真值表
正如我们在真值表中所看到,一个论证前提和结论的真值是与论证有关的真值函项联结词的规则赋予的。尽管这里只定义了五种真值函项联结词,但事实上,它们的总数是16个。这个数目是固定的。与之不同的是,可用于构造有效性证明的有效式和逻辑等价表达式的实际数目会因演绎系统的不同而不同。另外,证明程序并不规定从前提正确演绎出结论的步骤数:它取决于前提与我们决定采用的基本规则。
因为在这些方面,证明有一定的灵活性,所以在一个由基本规则构成的系统中,对于特定论证可以构造不止一个正确的有效性证明。也就是说,与真值表不同,一个证明并不总能在固定步骤内得出一个结论的机械程序。除此之外,为特定有效论证构造证明时,我们可能错误地评价了它的有效性。有可能当时“没有看出”使用特定规则可以从前提演绎出结论,错误地认为论证无效。这就是为什么,任意有效论证在“原则上”有一个有效性证明。然而必须承认,证明在某一方面确实优于真值表:当一个论证涉及很多种命题时,真值表往往会很长而且很不方便。证明就不会有这样的问题。
