各位亲爱的读者,我相信因为前面已经有了一次时间膨胀(时间变慢你也可以理解为时间膨胀了,这种说法比较酷,很多书都喜欢这么说,我也继续附庸风雅)的神奇经历后,再看到这个空间收缩的结论时,你已经能平静地接受了。那让我们来算一下,这个空间收缩的效应跟速度的关系到底有多大,不举一些例子相信你们始终没有一个直观的感受。一辆时速300千米的高铁火车从你身边开过,它的长度会收缩多少呢?一算,大约收缩了10-13米。这是多少呢?差不多就是一根针尖的千万分之一长度,人类到目前为止还不能测量这样的精度呢。但是如果你能坐上一艘速度为0.99999c的宇宙飞船,那收缩效应就可观了,你地面上的亲人将看到“压缩”了224倍的你和飞船,你和飞船都变成一个很扁很扁的玩具模型了;但是在飞船中的你,却不会有任何感觉。我们所说的收缩,是指一个参考系相对于另一个参考系的收缩效应。飞船没有发射的时候,你拿一把尺子丈量出飞船的长度是10米,飞船飞起来后,你用这把尺子一量还是10米。尽管地面上的亲人看到飞船“压缩”成了玩具模型,但你的这把尺子也同样缩短了,随着你的宇宙飞船运动的一切物体都缩短了。
我们勤奋的小爱已经通过两个基本原理,推导出了同时性的相对性、时间膨胀、洛伦兹变换、空间收缩这几个推论,但他并没有停止他非凡大脑的思考活动,紧接着又从洛伦兹变换推导出了新的速度合成公式,这个公式可以解决你脑袋中可能冒出来的若干疑惑。比如第一个疑惑:如果两艘宇宙飞船一艘朝东飞,一艘朝西飞,飞船的速度都达到了0.9c,那么从其中一艘飞船看另外一艘飞船,岂不是另一艘飞船的速度可以超过光速c了吗?第二个疑惑:如果我从一艘速度达到0.9c的飞船上再发射一艘速度为0.9c的飞船(或者导弹)出去,那地面上看到的第二艘飞船(或者导弹)的速度岂不是也应该超过光速c了?之所以还有这样的疑惑,那是因为牛顿时代建立起来的速度合成公式w=u+v(此处的w代表合成后的相对速度),在你的脑海里仍然是一个天经地义的常识,而且根深蒂固。但是牛顿的经典物理学已经在爱因斯坦的两个原理下崩溃了,几乎所有的公式都需要修正,都需要考虑光速这个看似不搭界的东西。让我们来看一下爱因斯坦推导出的新的速度合成公式是怎样的:
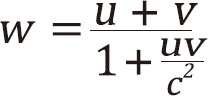
你仔细一看就会发现,当uv远小于c时,这个公式就近似等于经典速度合成公式。那让我们用这个新公式来解决一下你上面的两个疑惑吧:
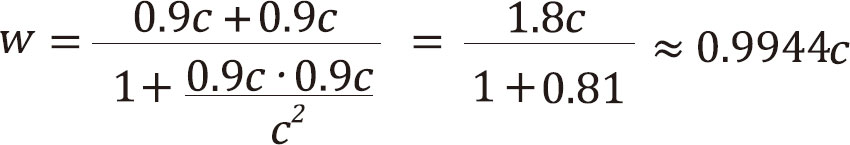
看,不论你速度多快,两个速度的合成速度最终都超不过一个c,哪怕两束光背道而驰,利用这个速度合成公式简单一算,结果最多也还是c。当然了,其实这个公式本身就是在光速不变的基础上推导出来的。但这绝不是文字游戏,这叫作物理公式的“自洽性”,也是非常重要的一条物理定律法则。
到此,爱因斯坦对自己的思考和得出的推论比较满意了。他把抽屉里演算用过的草稿纸都翻了出来,还好,最关键的几张都还在,没有被卷上烟丝当香烟抽掉(爱因斯坦有用草稿纸当卷烟纸的习惯,以至于他当初演算的众多草稿纸都这么被白白烧掉了。从今天的眼光来看,这烧钱烧得可够厉害,如果保留到现在,每张草稿纸都准能在拍卖会上卖个好价钱)。爱因斯坦整理了一下自己的劳动成果:
1.相对性原理:在任何惯性系中,所有物理规律保持不变。
2.光速不变原理:光在真空中的传播速度恒为c。
3.同时性的相对性。
4.洛伦兹变换。
5.时间膨胀。
6.空间收缩。
7.新的速度合成公式。
爱因斯坦用5周时间把以上这些成果写成了一篇论文,题目叫作《论运动物体的电动力学》。在这5周时间里,爱因斯坦的快乐心情无法言表,他对专利局的好兄弟索特(经常与爱因斯坦探讨物理学问题)只说了一句话:“我无法表达我的快乐。”1905年6月底,爱因斯坦将论文投给了德国的学术期刊《物理学年鉴》(这份期刊上还发表过爱因斯坦的许多著作)。该刊物负责理论的一位编辑——大物理学家普朗克(Planck,1858-1947)对文章中的观点感到非常吃惊,虽然与自己的概念相冲突,但开明的普朗克依然大胆地决定将论文发表出来,并且在日后,他成为相对论在科学界得到承认的过程中最重要的人物之一。
各位读者,请特别注意,到此时“相对论”三个字还没有正式出生,更不要说本章的标题“狭义相对论”五个字了。笔者正是要牢牢抓住你的这个好奇心,放到本章的最后再来解释为何要加上“狭义”二字。
论文虽然发表了,但是爱因斯坦自己心中的一个困惑始终还没有解开,总是搞得他茶饭不思,连晚上做梦也总在想:如果物体的运动速度超过光速会怎么样?从公式上看,会得到一个虚数,但虚数是一个数学概念,它到底有没有实际的物理意义呢?爱因斯坦非常纠结,不论他怎么做思维实验,总会遇到虚数这个数学怪兽跳出来挡住去路。
但爱因斯坦终究是爱因斯坦,此时的他已经打通了六脉中的三脉,虽然离最终神功炼成还有10年的时间,但仅凭这三脉神剑也让他成功地战胜了这只数学怪兽。且让我们来看一看,爱因斯坦是如何用一招“质速神剑”一剑封喉的。
