为了能让各位读者更好地理解爱因斯坦这神奇的一招,请让我们一起来回忆一个最基本的物理规律——动量守恒。还记得我们小时候打玻璃弹珠吗?如果你用你的玻璃弹珠把对方的玻璃弹珠打飞至一定的距离,你就可以赢得那颗打飞的弹珠。每一个打玻璃弹珠的人都会有一个自然的体会,那就是自己的弹珠越重、打出的速度越快,则对方的弹珠就会飞得越远。但这里面还有些特别的技巧要掌握:首先,你要正面击中对方的弹珠,如果打偏了效果就不好;其次,如果你能打出一个“旋转弹”,则这个弹珠打到对方的弹珠后,会停在原地旋转,而对方的弹珠则会滚得很远。这里面的道理就是动量守恒定律。在一个理想化的状态下,如果你的弹珠质量是m1,弹珠出手的速度是v1,对方弹珠的质量是m2,对方弹珠被撞后的速度是v2。假设对方弹珠被撞击后,你的弹珠停在原地不动,则符合下面的关系式:
m1v1=m2v2
这便是动量守恒定律。由这个最基本的动量守恒的公式,我们还能得出另外一个含义相同的公式。比如有一个物体的质量是m0,以速度v0运动,在运动途中由于某种原因(比如某个定时断开的机关)突然一分为二,分成两个质量为m1和m2的物体,分开后的速度分别为v1和v2,则它们之间也要符合动量守恒定律。如果用公式写出来就是这样:
m0v0=m1v1+m2v2
爱因斯坦把玩着这个公式,突然想到:根据用洛伦兹变换推导出的新的速度合成公式,两个物体的合成速度不可能无限增大,而是会随着接近光速而递减,那么为了满足动量守恒,质量m的数值就必须增大。爱因斯坦想到了马上就动手,他很快就利用洛伦兹变换和动量守恒定律得到了下面这样一个公式:
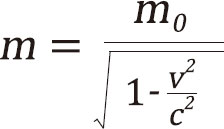
我们又看到了熟悉的相对论因子,这个公式改写一下就是:
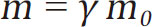
这个公式正是爱因斯坦解决超光速问题的神奇一招——“质速神剑”,通常我们也把它叫作“质速关系式”,就是说明质量和速度的关系。这个公式中m0表示物体相对静止时的质量,m表示物体以速度v运动后的质量。一看到m0旁边有我们的老朋友γ,你一定能马上反应过来,这就是说物体的运动速度越快,质量就越大。
牛顿如果地下有知,必定又会睁大惊恐的眼睛,暴怒道:“这个世界疯了!”在牛顿力学中,所有的定律都隐含着这样的一个前提,那就是物体的质量是不变的。我们用小球做实验,不管这个小球是在岸上还是在船上,不论是在实验室里还是在山顶上,它的质量是多少就是多少,根本不需要我们去重复称量。现在,爱因斯坦居然告诉我们,物体的质量并非是恒定不变的,质量也是相对的,就跟没有什么绝对的快慢,没有什么绝对的长短一样,对不起,也没有什么绝对的质量大小。刘慈欣在他的科幻小说神作《三体》三部曲中,描写了一个外星文明用一个玻璃弹珠大小的物体,击毁了另一个外星文明的“太阳”,其中的理论正是这个质速关系式。当“玻璃弹”的速度接近光速的时候,其相对论质量就会变得无比巨大,足以击毁一颗恒星(有兴趣的读者可以去读一读《三体》这部中国科幻界的扛鼎之作)。
我已经听见了你的嘀咕声:“喂,跑题了,你还没讲清楚为啥爱因斯坦用这个质速关系式杀死了那只数学怪兽,这个公式跟超光速到底有什么关系嘛?”抱歉,我一想到《三体》就开始神游宇宙。还记得牛顿第二定律吗?物体的加速度和受到的力成正比,和质量成反比。通俗地讲,就是你要把一个物体推得运动起来,物体质量越大你要用到的力就越大,想想看,质速公式告诉我们,物体的速度越快,则质量就越大,那么要推动它加速的力就必须越大。当物体速度无限接近光速,质量也会逐渐变得无穷大,那么显然要推动它继续加速的力也必须变得无穷大。对不起,无穷大的力是不存在的,谁也不可能创造无穷大的力,你就是把全宇宙的能量都集中起来,那也比无穷大要小。这就证明了没有任何有质量的物体的运动速度能达到光速,达到都不能,更别说超过了。那光本身呢?因为光在静止时没有质量,所以它能达到光速。
