没有什么比接受忠告更让人受益,即便最终事与愿违,(听取忠告)这一选择仍然是正确的。
11.1 对理性的正式定义
我们前面反复提到理性选择的过程,现在就重点谈一下理性(规范)决策理论。一些学者将理性(rationality)定义为选择和价值的兼容:理性行为是指使决策结果取得最大价值的行为。但是现在必须澄清的是,要回答价值的构成并非易事,并且我们认为选择之理性与选择的过程有关,而与选择的结果无关。尽管如此,决策理论的一些重要研究还是将注意力放在了考察决策与决策者价值观的关系上,这就是John von Neumann 和 Oskar Morgenstern(1947)的工作。相关的经典论述主要出现在《博弈论和经济行为》(Theory of Games and Economic Behavior)一书中,他们所提出的期望效用理论(expected utility theory)是数学和行为科学中关于理性选择最通用的解释。本章我们会介绍这个理论,并与心理学中的决策行为联系起来。
本书曾多次提到,我们(以及大多数心理学家)认为理性理论至多是对个体实际行为的近似描述。尽管大部分人似乎都能意识到实际行为和理性标准是分离的,人们仍然希望做出明智决策,避免在推理和行为之间出现矛盾,使自己的行为符合期望效用理论提出的理性原则。正如我们不了解概率论一样,人类这个物种也并非生来就了解这些理性原则,这就是为什么我们要研讨von Neumann和 Morgenstern提出的理论——它不是与生俱来的,我们必须研究它,理解其对行为的影响。因此,我们会特别介绍如何运用期望效用理论来提升决策质量。
von Neumann和Morgenstern(1947)的理论阐述是纯数学化的。他们指出,如果决策者的选择遵循特定的(理性)规则(“公理”),那么由此可引申出效用(utility)的概念,即用实数来量化个人价值。每个选项通常都包含多个概率结果,当且仅当一个选项的期望效用(expected utility)大于另一选项时,决策者才会更偏好这个选项。下面我们分步进行分析:
1.每个选项由多个概率结果组成。首先我们假设,决策者在不同选项间进行选择时,会遵循我们定义理性时所用的“公理”;
2.于是我们可以用一个实数来代表选项中每个结果对决策者的效用;
3.某一特定选项的期望效用指的是对这些数字的期望,即选项中每个结果对应的数字由每个结果所发生的概率加权后的总和;
4.得到结论:当且仅当选项X的期望效用(实数)大于选项Y时,决策者才会更偏好X。
上述公理化系统实现了几个重要目标。首先,它简明扼要阐述了理性决策的一系列原则。当然,即使在规范的哲学水平上,这些原则也仅是对理性决策本质的一个假设。尽管有哲学家和数学家也提出了一些其他理论,von Neumann 和Morgenstern的理论目前无疑是描述理性决策的最佳理论。其次,如果这些公理的条件成立,那么一定可以建构出一种效用度量,由实数所表征的不同结果价值可以进行排序比较,由此我们就可以建立一种类似物理学中衡量物体质量的量表,这必定会促进科学研究和实际应用的发展。(可以想象一下如果在现代物理学、化学和工程学中不存在度量的话,将会是怎样的一种状况。)第三,尽管我们还没有对这些公理进行详细的阐述,但总的说来可以根据个体对不同结果的偏好程度,对效用进行衡量。
许多研究价值和行为关系的决策理论家认为,理性是指做出的选择符合上述公理,同时他们进一步假设,该公理也适用于个体实际选择的情形。当且仅当选项X的期望效用大于选项Y时,理性的决策者才会选择X。当然,这并不是说我们的决策就完全符合这些公理的描述,它只是提出了一种理想化的理性选择假设。实际上,正如我们在前十章提到的判断和选择的心理学研究结果那样,在许多决策情境下,个体实际的行为往往并不符合这些公理。
同样,在von Neumann和Morgenstern(1947)的期望效用理论中,并没有阐述人们决策时会考虑结果的效用。效用是一个纯数学的概念,是由公理定义产生的——就像几何学中三角形的边和角,也是由几何学系统下的公理定义所产生的数学概念。然而,我们会将几何学中点和线的抽象概念与物理世界的点和线对应起来(比如在纸上或在脑中形成图像),同样,抽象的效用概念也会与决策者的个人价值观对应起来。因为人类与物质世界(几何学与之有关)不同,具有主观能动性,因此从分析(analytic)和综合(synthetic)这两种视角出发对这些公理进行解释就会出现困惑。如果从分析的角度来解释期望效用理论(经济学家通常持有这样的观点),实际的选择可以解读为对个体偏好的反映,而偏好又能进一步被解读为是效用的反映。这似乎有点因果颠倒,就像心理学家Lola Lopes(1994)提到的,“根据现代的[分析性]观点,效用并不是偏好的前因,只是因为有些决策者,有意也好无心也罢,遵循了von Neumann 和 Morgenstern提出的公理体系下的决策原则,为方便研究者总结这些决策者的偏好,就生造出这样一个概念”(p.286)。
相反,期望效用理论也可以从综合的角度进行解读。首先我们要对某个选项的效用和发生概率进行判断,然后根据公理阐述的原则,将二者结合后进行比较,预测出最终的决策。对于大多数人来说,上述顺序很易理解:我们决策时,首先要清楚我们想得到什么以及怎样得到它,接下来才能决定要采取怎样的行为或做出怎样的选择——先确定目标和价值,再有选择和行为。而分析的视角则认为我们先观察到自己的选择,再推断我们的偏好,看起来顺序就反了。不过也有例外的情况,比如在心理分析领域,我们就试图从自己的行为出发,分析性地探索出这些行为隐含了什么期望和信念。同时,值得我们注意的是,分析的视角与综合的视角同样有效,并且在数学和经济学这两个最为关注期望效用理论的领域中分析视角比综合视角更受青睐。
然而,Tversky 和Kahneman(1974)在一篇经典的文章中指出,甚至可以先估算概率,再“用来”指导决策。他们的叙述如下:
值得注意的是,在打赌下注时,虽然有时可以从偏好来推断主观概率,但通常并非如此。一个人在A队和B队的比赛中买了A队赢,是因为他认为A队获胜的可能性更大,而他的结论并不是从他买A队赢的这个下注倾向中得到的。因此,实际上,是主观概率决定了下注偏好,而不是理性决策的公理性理论所说的那样,偏好决定了概率。(p.1130)
经济学早期关于效用的定义(比如Jeremy Bentham[1789/1948]的观点)带有心理学涵义,但现代效用理论则舍弃了绝大多数的心理学成分,只保留了“个体所选即所好”这一行为原则。然而,在过去的十几年间已经发生了重大的变化,一些行为学家,比如Daniel Kahneman、Colin Camerer、George Loewenstein和David Laibson等,关注到了价值判断的认知和情绪来源,他们用这些心理学内容丰富了经济学的概念体系。
我们通常说的“个人价值观”(personal values)这一概念比von NeumannMorgenstern理论中提到的“效用”概念具有更丰富的内涵。比如,我们认为某些个人价值观或价值体系可以用语言来表达,而未必要通过实际行为来推测,否则,在我们的语言体系中就不会出现“伪善”这个概念,伪善指个体所声称的个人价值和特定行为存在不一致。同时,我们还认为价值观是独立于语言和行为而存在的。在平常的语言中,我们认为价值是一种重要的存在维度,在这个维度上可以有客体、行为或者是其他的现象。比如,我们说“他看重自由”就和说“他昨天去上班了”一样稀松平常。事实上,我们陈述价值观时常常就像在陈述一个一般事实,即便很多哲学家在事实和价值这两类陈述之间做了明确的区分。而只有在学习过哲学之后,大多数人才开始对自己和他人所看重某些事物或行为产生困惑。(一些逻辑实证主义者曾指出,关于价值观的陈述都是主观任意的,或者说至少这些陈述是没有实证证据支持的。)或许我们在平常说话和思考时应该更谨慎一些。(这是另一种价值观!)在第9、10章提到的一些研究提醒我们,关于个人价值观的许多直觉性判断是值得怀疑的。
价值观的另外一个特点是不依赖于特定的情境。当我们提到自己看重某些东西的时候,并不是特指与某个特定情境相关联的行为、感受和信念。比如,“他看重自由”这个说法,能够整体概括性情、行为和信念,并且如前所述,我们用语言至少可以模糊地将这种概括陈述出来。有一个流行的人格测验——罗基奇价值观量表(the Rokeach Values Inventory)就是以语言概括的方式来测量个体的价值观,这个量表要求受访者对一组抽象的价值条目进行排序,如平等、自由、家庭安全、智慧、宗教救赎等,然后根据排序的结果预测个体的行为。举例来说,如果受访者将平等排在前面,那么他们很可能支持在学校中取消种族隔离、开展反歧视行动、优待少数民族等政策;将宗教救赎排在前面的受访者很可能常常会去做礼拜。(我们可以推测,罗基奇测验的预测力源于信念抽样模型的一些原则。我们在章节9.5中讨论过,信念抽样模型主要用来建构总体价值观,一些相互关联、具有评价含义的信念形成一个价值观总体,当我们处于相关的情境[如刚刚有人恳请你在平权请愿书上签名]中时,总体中的某些价值观标签[如“平等”]就被抽样出来。因此,测验对行为的预测力就取决于经由价值线索提取出来的各种记忆的重合度。)
11.2 使理论更容易理解——公理法
据我们所知,希腊数学家欧几里德是第一个将理论(对于他来说主要是关于几何和数字的理论)总结为一种简洁优美的公理体系的科学家。这种方法的核心思想是,某种理论的重要假设可以抽取出来并以精确的符号体系进行表述,然后从这些公理出发可以推导出核心理论的一些推论(如定理)。使用这种方法对理论进行表述的优点很多:理论家们可以对初始理论的完整性和一致性进行检验;科学家在应用、检验或修正理论的时候能够聚焦于核心内容;对于不符合理论假设或理论推导的情况可以以一种系统有效的方法加以解决。但是,公理法的运用仅局限于数学领域,在科学界并不普及。在行为科学理论中,效用理论是使用此方法的范例,这一点使它优于其他表述混乱的理论。
作为公理系统的von Neumann-Morgenstern理论衍生出了数字效用。该理论受到了行为科学家们的特别关注,因为其结论对于决策和价值观具有重大意义,特别是要在日常生活和语境中理解这些术语时。正如欧几里德几何理论的结论可以应用于现实世界的物体,我们推测期望效用理论的结论也可以描述或对比实际的决策行为——如若不然,它们就会变成纯粹的规则系统,玩弄数字和符号,丝毫引不起我们的兴趣。
为了探讨该公理体系的性质及其与实际的联系,我们将引入另外一种更简单清晰、同时可以类比von Neumann和Morgenstern理论的体系。在此,我们选择的是物理学中物体的质量。表征质量的一般都是正实数,数值可以相加,比如将一个137克的质量和一个786克的质量一起放在天平上,就会得到923克的质量。同时,这样的实数也具有其他一些重要的性质,下面将一一陈述:
性质1:可比性。任意两个正实数之间都可以进行大小比较。若用x和y分别代表不同的正实数,则两者的关系只有三种:x 〉y,y〉x,或x=y。为了简化描述,不再分别描述相等和不相等的关系,我们可以使用一种“弱强度”的形式来描述可比性,即“大于等于”(≥)。于是可比性可以表述为:对于任意两个正实数x和y,要么x ≥ y,要么y ≥ x,要么前述两种关系同时成立(即相等)。
性质2:顺序性。“大于等于”的关系决定了数值之间大小顺序的可传递性,即如果 x≥y且y≥z时,那么x≥z。
性质3:加法运算的封闭性。两个正数相加会得到一个新的正数,即x和y都是正数,那么它们相加的和z = x+y也是正实数。
性质4:加法的结合律。多个实数相加,相加的顺序不重要,即x +(y+z)=(x + y)+ z。
性质5:加法的交换律。两个实数相加,它们位于加号前后的顺序对结果没有影响,即x+y = y+x。
性质6:可化简性。两个实数同时加上第三个实数后,其大小顺序不变,即当且仅当x ≥ y时,x+z ≥ y+z成立。
以下两条性质的提出更多是出于数学上的考虑。其中阿基米德性质(但它是由欧几里德提出的)指出,不存在一个绝对大或绝对小的正实数,即不管一个数比另一个数小多少,总会存在一种情况使得小数乘以某一正整数后大于另一个数。
性质7:阿基米德性质。对于两个任意的实数来说,它们之间总会存在一种大小关系,但是这种大小关系并不是绝对的,当较小的数与某个正整数相乘后就可能大于较大的数,即如果x ≥ y,那么就会存在整数n,使得ny>x。其中,ny代表的是n个y相加;同时,这条性质与一般意义上的乘法运算联系不是很紧密,因为当我们将两个数结合在一起的时候,并不一定需要/必须通过乘法的方式实现。(由此,我们可以得出结论说并不存在绝对大或绝对小的正实数:任意选择两个实数x和y,其中x ≥ y,但x并不是最大的数,因为存在整数n,使得ny〉x,同理,y也不会是最小的数,因为存在同样的n,使y〉x/n。)
性质8:可分解性。如果x ≥ y,那么存在另一实数z,使得x〈y+z。
德国物理学家和数学家Holder认为物体在天平上的状态完全符合上述8条性质,其中x R y表示物体x比物体y重(R就相当于数学上“〉”的关系),操作O表示的是将两个物体放在天平的同一端(将它们串联在一起)。读者必须牢记Holder的观点以及R和O代表的含义。(当然,这种类比只是概念上的,因为天平是有一定量程和测量误差的。)鉴于此,Holder仅在数学层面上将自己的公理体系与实数的性质进行类比,并找到了二者的相似之处。他最后得出结论,认为可以用某种度量单位来表征天平上的物体,在这里,这种量度就叫做质量。
Holder于1901年的发现意义更为重大。他借鉴数学的分支之一计量理论中的观点指出,如果某一体系具有上述8条性质(“符合公理所述”),那么就可以将体系中的元素与实数联系在一起,同时,这些实数除了可以乘以正的常数外,还是很特别的。(具有上述属性的量表称为等比量表。)也就是说,他在自己的公理体系中重述上述8条性质,同时指出R和O分别代表的是数学中“≥”的关系和相加的操作。他又进一步指出,如果某一体系中的各元素之间的关系和相加操作符合上述8条性质,同时(1)可以用x R y表示x ≥ y,(2)用z = x O y表示z = x+y的话,就可以赋予各元素不同的实数。而且,对于同一体系中的两个不同的度量单位来说,它们之间存在一种正乘数的关系,比如,1千克=1000克。这些数字被称为度量,度量与实体x联系在一起用m(x)表示。正如实数的单位是1,在质量中,我们用标准克或标准盎司作为基本单位(克与盎司之间有一定的乘数关系),这符合先前得到的结论,即对于同一体系中的两个不同的度量单位来说,它们之间存在一种正乘数的关系。
11.3 对理性的定义:期望效用理论
公理法是一项伟大创举,因为它将某种理论的本质简化为一些假定,这些假定只包含有该理论得以衍生的全部必需的定义和假设。尽管这一方法在科学领域还未得到普及,但是我们有理由相信使用此方法来阐述理论是我们应该追求的最高境界。即便我们已经使用等式、计算机程序模拟或语言等对某一理论进行了精确描述,但为了更好地理解和评估理论,对核心原则的总结是绝对必要的(参见Hastie & Stasser, 2000)。通常,我们可以提出各种不同但逻辑等价的公理法,并不存在一种具有普适性的公理法。如前所述,我们提出实数的8条性质及由此引申出的有关重量的一些原理,主要为了方便读者的理解。也有学者使用另外的体系,其中大部分更为简练,但是可能只有相关领域的专家才能理解。以von Neumann 和 Morgenstern的效用理论为例,不同的人会使用不同的公理法对其进行解读,但是我们采用这种方法,即使读者对数学逻辑知之甚少,也能够理解。
von Neumann-Morgenstern理论的基本元素(entities)可以概念化为一些可进行评估和选择的选项(alternatives),这些选项由一些以不同概率出现的结果组成,通常被称为赌博(gambles)。基本的关系用偏好(preference)来表示,依据偏好可以对选项排序;弱排序(weak ordering)(≥)在这里代表的是行为上的“无所谓或更偏好”。(这种表达方式比较粗略,将≥解释为“不是更偏好”更加准确,因为A≥B和B≥A可以同时存在,即A~B,但是这种表示方法比较尴尬,强偏好[〉]和弱偏好[≥]的区分在技术上更精确,读者们可以根据自己的习惯选择区分或不区分。)
将不同选项组合起来的基本操作(operation)(相当于将不同的物体放在天平的同一端,即串联[concatenation])可以概念化为不同选项出现的概率混合(probability mixture)。因此,如果A和B是两个不同的选项,ApB表示的是选项A出现的概率是p,选项B出现的概率是(1-p)。可以看出,B的概率是隐含的,我们仅仅考察只存在两个选项的选择,因此,当赋予A出现的概率为p时,那么B出现的概率就是1-p,或者是余数(complement)。
为了对公理进行详细阐述,我们现在假设一种复杂的、多步骤的赌博情境。对于出现的结果,我们将分别在每一个公理下进行详细描述(尤其是公理3“封闭性”和公理4“概率的分布”。)因为不同的选项包含有不同的结果,而这些不同的结果又具有特定的出现概率,所以选项的概率混合与结果的概率混合是等价的;也就是说,如果选项A包含两种结果x和y,它们出现的概率分别是r和(1 - r),选项B由结果z和w组成,出现的概率分别是s和(1-s),那么ApB包括概率是rp的结果x,概率是(1-r)p的结果y,概率是s(1-p)的结果z和概率是(1-s)(1-p)的结果w。只包含有一个结果的选项的意思是该结果出现的概率是1。
我们发现,如图11.1所示用决策树图解模式来表示选项、结果和概率混合非常有助于理解。当需要对理论上的赌博情境进行比较(比如,通过比较来掌握某种公理的实际意义或不同实验条件下赌博情境的结构),尤其是要将理论体系应用于实际决策时,这种方法非常有效。
von Neumann和Morgenstern(1947)证明了公理条件成立时,就可以对不同结果进行赋值,这个数值就是效用(类似于用重量对物体进行数值表示),同时可以依据期望效用值的大小对选项进行排序。换言之,我们对选项的偏好强弱可以用它们的期望效用排序表示。(因为当选项中只存在一种结果时,该结果发生的概率是1,此时结果和选项是等价的,反之亦然,所以我们既可以使用结果,也可以使用选项来对公理进行阐述。但为了便于理解,我们还是选择用选项对公理进行阐述。)
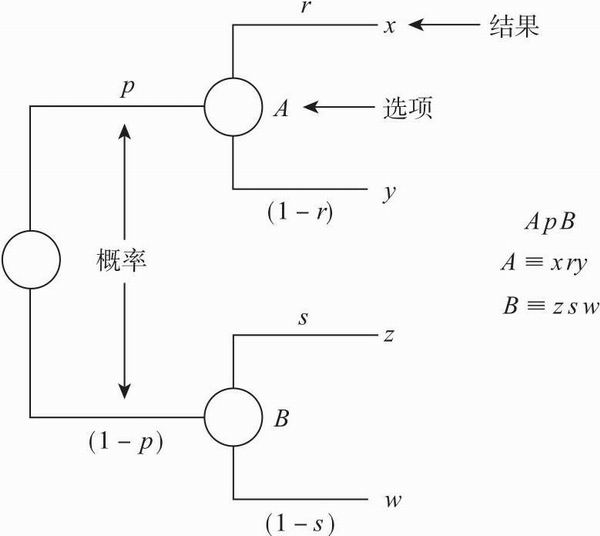
图11.1 用决策树简化的赌博情境范例(对von Neumann和Morgenstern理论的简化)
我们可以将von Neumann和Morgenstern的理论和Holder关于质量的理论作如下类比:将选择中的不同选项类比为质量未知的不同物体;将强度较弱的偏好比作天平上一种质量“大于或等于”的相对状态;“概率混合”这种串联性的操作(即在一个只存在两种结果的赌博情境中将两个选项联合在一起)就相当于将不同的物体放在天平的同一端。在上述两种理论体系中,如果理论假设成立的话,结果就产生了一个可以测量效用或质量的实数量表。
最后,我们对von Neumann和Morgenstern期望效用理论的内容进行介绍:
公理1.可比性:如果A和B同时存在于选项集S中,那么它们之间的关系是A B,B
B,B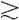 A或上述两种关系情况同时成立,即A~B。
A或上述两种关系情况同时成立,即A~B。
公理2.传递性:如果A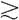 B且B
B且B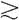 C,那么A
C,那么A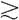 C。
C。
公理3.闭合性:如果A和B同时存在于选项集S中,那么ApB也存在于其中。
公理4.选项间概率的分布:如果A和B同时存在于选项集S中,那么[(ApB)qB] ~(ApqB)。
公理5.独立性:如果A、B和C同时存在于选项集S中,那么当且仅当(ApC) (BpC)时,A
(BpC)时,A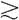 B。
B。
公理6.一致性:对于选项集S中的所有结果来说,用A和B代表两个不同的结果,则有当且仅当A (ApB)
(ApB) B时,A
B时,A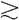 B。
B。
公理7.可分解性:对于选项集S中的所有结果来说,用A、B和C代表三个不同的结果,则有当A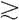 B
B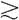 C时,存在一个p值,使得B ~(ApC)。(这条公理对于编制测量效用的量表非常关键。)
C时,存在一个p值,使得B ~(ApC)。(这条公理对于编制测量效用的量表非常关键。)
如果用实数来代表不同的选项及其概率值,那么只有当代表选项的实数值大小等于期望时,才满足公理。但是von Neumann 和Morgenstern(1947)却是从相反的逻辑进行证明,如果上述公理成立,就能构建一个量度,每个选项等于期望,就可按期望值大小对选项进行排序。同时,我们可以任意确定该量表的原点和单位(就像确定我们熟悉的温度计的原点和单位)。代表选项的实数值称为期望效用,代表结果的实数值称为结果的效用,如果一个选项只包含一个概率为1的结果,那么代表结果效用的这个数字就等价于选项的期望效用。因为只有测量效用的量表的原点和单位是任意的,所以任何不同的测量都是有线性联系的,也就是说,任意两种不同的测量系统得到的结果在二维直角坐标系中都会呈线性关系。这种量表称为等距量表,它的原点和单位都是不确定的(质量量表是等比量表,因为它的原点不是任意的,而单位[如,克、盎司]则是任意给定的。)
原点和单位的不确定性使得我们可以根据两个选项已知的效用值计算出第三个选项的效用值,这主要利用的是公理7“可分解性”。假设A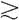 B
B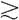 C,同时A的效用值为100,C的效用值为0,根据可分解性的公理描述,存在一个概率值p,使得B等于ApC,其中ApC表示的是p个A的效用值加上(1–p)个C的效用值,即p100 +(1–p)0。因此,如前所述,可分解性公理对于得到具体的效用值非常重要。因为所有量表的效用及度量之间是线性的关系,所以我们可以假定100代表最为偏好的选项的效用值,0代表最不偏好的选项的效用值,那么在此前提下,就可得到其他选项的效用值,这些值位于0到100之间。我们注意到对于概率的测量有助于我们得到具体的效用值。(如果“满足公理”,概率的规则和度量将会在决策者的偏好中有所体现——但是,假如我们在前十章中提到的实证结果有效的话,这一点在行为上很难实现。)
C,同时A的效用值为100,C的效用值为0,根据可分解性的公理描述,存在一个概率值p,使得B等于ApC,其中ApC表示的是p个A的效用值加上(1–p)个C的效用值,即p100 +(1–p)0。因此,如前所述,可分解性公理对于得到具体的效用值非常重要。因为所有量表的效用及度量之间是线性的关系,所以我们可以假定100代表最为偏好的选项的效用值,0代表最不偏好的选项的效用值,那么在此前提下,就可得到其他选项的效用值,这些值位于0到100之间。我们注意到对于概率的测量有助于我们得到具体的效用值。(如果“满足公理”,概率的规则和度量将会在决策者的偏好中有所体现——但是,假如我们在前十章中提到的实证结果有效的话,这一点在行为上很难实现。)
从构念上来说,von Neumann 和Morgenstern的理论体系是完美的。虽然可能会显得很罗嗦,但我们还是要再次强调,通过分析公理衍生出的“效用”与我们直觉上或言语中提到的“个人价值”是不吻合的,这不同于对于物体重量的判断,通过客观标准(天平的倾斜)和主观标准(直觉)得到的结果相差无几。不过,如果我们说质量这样的概念与日常生活中重量的直觉毫无关联,人们一定会觉得奇怪,同样,效用的概念看起来和主观价值理应存在关联。实际上,正因为从von Neumann 和Morgenstern的理论中衍生出的效用与主观的价值判断之间确实存在关系,所以它才吸引了心理学家的关注。也是基于这一点,我们试着在本章结尾提出一些可能提高决策质量的方法。也许初步思考后,大部分人会意识到每一条公理的内容都能反映理性的某一侧面,甚至能对个体如何选择进行描述。我们接下来要对每个公理进行详细分析:
公理1.可比性:如果A和B同时存在于选项集S中,那么它们之间的关系是A B,B
B,B A或A~B。
A或A~B。
公理1主要描述人们面临两个选项时,相比较而言,决策者至少应该对某一选项表现出较弱的偏好。最极端的情况是决策者必须二选一。但是这条公理也能说明由于对两个选项都无所谓,所以无法做出选择。现实中是否存在这种情况呢?我们可以回想一下第10章提到的教授选择工作的例子,如果她难以抉择,是否就说明她对不同工作的态度是无所谓的呢?Jay Kadane,Mark Schervish和Teddy Seidenfeld(1999)的研究表明偏好不明显并不代表无所谓。在某些情境中,“保护性机制”发挥了作用,人们拒绝做出选择,这实际上也是种选择。Jonathan Baron 和 Mark Spranca(1997)引用了一些人们拒绝做选择的情形。比如,在一些涉及需对金钱和生命进行权衡的决策情境中,人们倾向于避免深入思考,“选择不做选择”。但是如果要人们在限速90公里下驾驶廉价汽车与交通事故造成 50 000人死亡之间进行选择,而最终的结果是“不做选择”,真的能说明人们无所谓吗?
苹果和桔子都是水果,如果必须在两种水果中挑选一种,最终的选择要么是苹果,要么是桔子。从分析的角度来说,选择本身是否不能定义偏好?经济学家将这种选择称为显示性偏好,同时假设从效用理论可以推导出来。比如,我们对于高速路上安全的偏好相当于认为每个人生命的价值为三百万美元。如果我们不知道为什么会做出这样的选择,其实在选择的时候就暗含有偏好的成分在里面。比如,我们在第10章提到选择工作的教授,她一时难以抉择,但是最终还是选择了离自己亲朋好友较近(或较远)的一份工作,与亲朋好友的距离不就是她最看重的因素吗?或许她并不能意识到或羞于承认此种原因,因为她觉得这样做理由并不充分。除了极个别的情况,比如抛掷硬币,我们认为在大部分情况下,人们都是有偏好的。但是,我们通常不太能接受显示性偏好的说法,即选择已经包含了偏好的成分,这一点在前几章已有阐述。具体来说,选择可能确实是非理性的,具有矛盾性。因此可以认为在特定情境中的选择和个体在此情境中的偏好可能是不相符的。
由于选择存在认知困难,显示性偏好也易受到批驳,但从外显证据推断偏好的最常见原因是:人们有时会做他们不想做的事,即我们选择了自己并不偏好的选项,比如,心理学家和哲学家威廉·詹姆士发现牙痛患者喜欢用舌头去舔疼痛部位,即使他们知道这样做会加重疼痛感。
但是,支持显示性偏好的理论家们认为舔牙痛部位的行为带给患者更多的是一种积极体验,而牙痛本身带来的则多是消极体验。当然,这种积极的体验看起来很“愚蠢”,因为患者只有通过治疗才能缓解疼痛,而舔只会使疼痛加剧。同时,他们认为“不同个体爱好不同,这一点是毫无争议的”,舔后带来的更强烈的疼痛感要比牙痛本身更被患者偏好。
因为我们不清楚构成个体高兴和痛苦的成分有哪些,所以用“个体有时会选择自己不喜欢的选项”这一事实来反驳显示性偏好理论是不充分的。但是,从认知的角度入手,指出选择的矛盾性,就能推翻这一观点。
公理2.传递性:如果A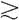 B且B
B且B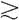 C,那么A
C,那么A C。
C。
捍卫公理2最首要的工作就是排除“钱泵”情形的产生。假设约翰在选项A、B之间,更偏好A;在B、C之间,更偏好B,但是在A、C之间,又更偏好C,进一步假设在任何两个选项之间他都不是无所谓的。结果就是他应该自愿地拿出一些钱,用偏好较弱的选项去交换得到偏好较强的选项。现在假定我们将选项C作为礼物送给约翰,由于在B、C之间,他更喜欢B,所以为了得到B,他就会拿出一些钱;然后用B去换A,也要拿出一些钱,同样用A换C,也需要钱。如果就此打住,约翰就得通过三次支付行为来得到一开始被当做礼物送给他的选项C。实际上,这是个无限循环的过程,约翰最终会花费很多的钱,但却得不到自己最想要的东西(当然这只是种假设)。
回应“钱泵说”的证据就是,具有传递性偏好的个体通常会拒绝玩这种游戏。除非在某些特殊条件下,选择并不会无限次重复。我们对两个选项中某一个的偏好并不是固定不变的。某人引用过一位著名经济学家的观点,在特定的决策情境中,大多数人“既会满足自己的偏好,又会让公理自证”(保罗·萨缪尔森,引自Daniel Ellsberg,1961)。比如,现在某公司需要招聘一位新秘书,对能力的要求有三点,(1)文职技能,(2)组织协调能力,(3)愿意承担职位描述中未涉及的其他任务。假设有三个应聘者符合条件,分别是A、B和C。其中在能力(1)上,优秀等级排序是A,B,C;同理,能力(2):B,C,A;能力(3):C,A,B。由此我们看出A在能力(1)和(3)上优于B,B在能力(1)和(2)上优于C,C在能力(2)和(3)上优于A。如果我们要两两比较做出选择的话,就会陷入无限循环中,且不符合可传递性的公理描述。(这就是我们在第10章提到的定性附加差异或投票法选择策略。)在这里,最关键的是三名应聘者被考察的顺序,最后被考察的人将会被录取。
这种结果必然是糟糕的吗?尽管理论上,人事经理会陷入“钱泵”的循环怪圈中,但是实际上并非如此,没有人会先随便指派给她一位秘书,然后根据上述排序,通过索要回报无数次地为她更换人选。当然,我们的亲身经历又告诉我们,当需要做出重要决定同时又极其困惑的时候,这种“钱泵”的现象还是存在的:“好了,我将选择那份薪水高的工作;但是第二份工作又比较的轻松,有很多灵活的假期;再等一下,我不想住在中西部,但是第三份工作能提供很好晋升的机会……”诸如此类的情形会使我们感到不适,难以抉择。
我们的观点是:选择应当具有可传递性。这主要源自某一著名论断,即从宏观全局的角度上做出的选择是最佳的。这一论断出自康德,他认为应该把做选择当成为所有人制定永久性的政策。实证证据表明如果判断选择质量的标准存在的话,依据康德所言做出的选择,确实要优于仅仅将眼光局限在当前选项之上而做出的选择。
公理3.闭合性:如果A和B同时存在于选项集S中,那么ApB也存在于其中。
公理3仅仅要求决策者将不同选项的概率混合当作一个选项来考察。如果做不到这一点,建构有关决策的理论将变得毫无意义。
公理4.选项间概率的分布:如果A和B同时存在于选项集S中,那么[(ApB)qB] ~(ApqB)。
从根本上说,公理4要求我们遵循概率论(见附录)。这条公理在图11.2和11.3有关决策树模型中已有所展示;为了使该公理成立,左边的二阶段赌博必须与右边的一阶段赌博是等价的。
当然,我们一般不会质疑该公理,但是实际行为却并非如此。比如,某人在两种不同的赌博情境中的表现是不同的,但是公理成立的前提是他应该具有不变的行为模式,这两种赌博情境分别是:(1)以0.20的概率赢得45美元,(2)在第一阶段有0.75的可能性未得到任何奖励,但是在第二阶段以0.80的概率赢得45美元。(因为[1.00–0.75]× 0.80 = 0.20,公理4要求我们在这两种赌博情境中的行为表现是相同的。)
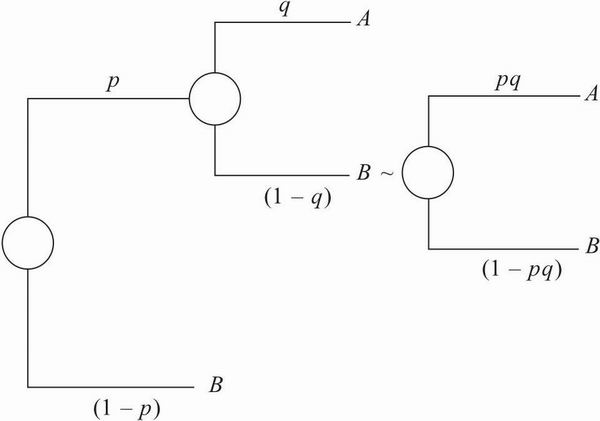
图11.2 用决策树表示公理4中提到的两种赌博情境
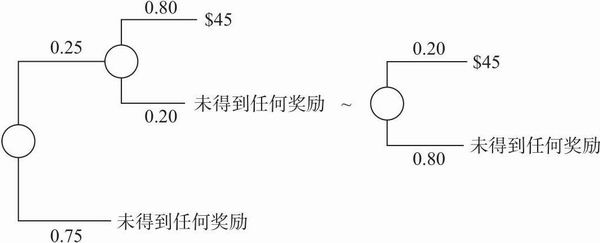
图11.3 用决策树表示由公理4引申出的具体实例
Von Neumann和Morgenstern(1947)在讨论概率的时候,假设它们是客观的。(尽管概率的准确性和客观性很复杂且具有争议,但是他们认为自己理论中涉及到的p和q都是通过绝对标准的测量得到的。)也有一些决策理论不符合这条公理,其中最值得一提的就是Ward Edwards的观点,他建议从客观概率转向主观概率,从而得到另一种理性决策理论。我们完全有可能得到同样满足概率论(在第9章和附录中都会提及)的非客观的概率混合。如果决策者要通过概率估计来解决未来不确定的问题,他的概率估计必须符合概率论的要求,否则,将会做出矛盾的选择。在第12章,我们将对预期理论(在第9章已提到)进行深入分析,预期理论是一种公理化的非期望效用理论,它使用的是非客观的、变化的“决策权重”而非“概率”的概念。预期理论在整体结构上与期望效用理论是相似的,但是,它只是对决策行为的描述,并非理性选择模型。
公理5.独立性:如果A、B和C同时存在于选项集S中,那么当且仅当(ApC) (BpC)时,A
(BpC)时,A B。
B。
公理5非常重要。实际上,许多决策理论家都曾详细地研究违背或删除公理5的影响有多大。乍一接触到这条公理,我们可能会觉得它的作用甚微:如果在两个选项中,决策者更为偏好其中的一个,那么即便存在某一特定的概率,使得决策者最终放弃了它们两个,而选择了第三个选项,但是在先前的两个选项之间,决策者的偏好是不是不应该发生变化呢?这就是公理5包含的主要内容,图11.4对其进行了解释。
注意:一些同学不太理解这条公理,因为他们错误地认为存在一种同时接受的情形,即选择者同时接受A和C或同时接受B和C,但是这里指的是接受A或C的一种概率混合与接受B或C的概率混合,“或”的意思是排太,在A和C、B和C分别二择一。如果公理描述的是一种同时接受的情形的话,就会说不太通:但是对于鞋子来说,我们却不希望仅仅得到一只鞋子,而能得到一双则是比较完美的。
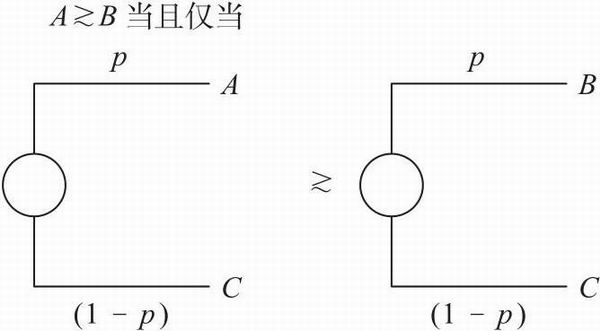
图11.4 用决策树模型对公理5进行解释
下面我们考虑一种假确定性效应:在有0.20的概率得到45美元和0.25的概率得到30美元之间,大部分人都更偏好前者(如图11.5中第一部分所示),而在100%能得到30 美元和有0.80的可能性得到45美元之间,也更偏好确定的前者(如图中第二部分所示)。接下来用A选项代表100%能得到30 美元,B选项代表0.80的可能性得到45美元,两者中更偏好A(如图中第二部分所示),再用C选项代表得不到任何东西,p值是0.25,那么,(A 0.25 C)表示的是100%得到30美元的概率是0.25,同时得不到任何东西的概率是0.75(如第三部分左半边所示),根据概率分布的原理,这也就相当于有0.25的概率得到30美元(如第四部分左半边所示)。相反,(B 0.25 C)表示的是有0.25的可能性以0.80的概率得到45美元,同时有0.75的可能性得不到任何东西(如第三部分的右半边所示),即共有0.80 × 0.25 = 0.20的概率能得到45美元(如第四部分右半边所示)。由此看出,大多数人在第一部分的偏好与第二部分的偏好实际上是相反的,因此,在前两部分同时出现典型偏好的个体(绝大部分人都会如此)就出现了假确定性效应,违背了独立性公理。
假确定性效应说明我们的选择受结果呈现方式的影响,而非结果本身的影响。这种非理性的行为是反驳独立性公理的唯一证据吗?答案是否定的。公理5暗示出决策者是不会受到结果偏态性(skewness)的影响的,这种偏态性主要针对的是有关个人价值观的概率分布。图11.6显示的就是两个不同选项的偏态分布。两个分布的均值相同,即个人价值的期望值是相同的,根据公理所述,最终的选择主要依据的就是这一期望值。这两个分布的方差也相同。(关于概率分布均值、方差的描述可以参考基本的统计教材,如Freedman、Pisani、Purves和 Adhikari于1991年写的《统计学》[Statistics]。)
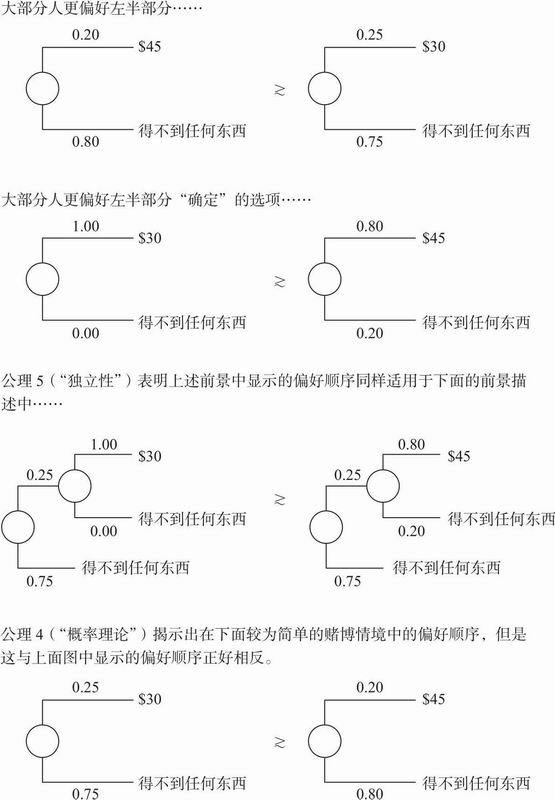
图11.5 违背公理4和公理5的假确定性效应
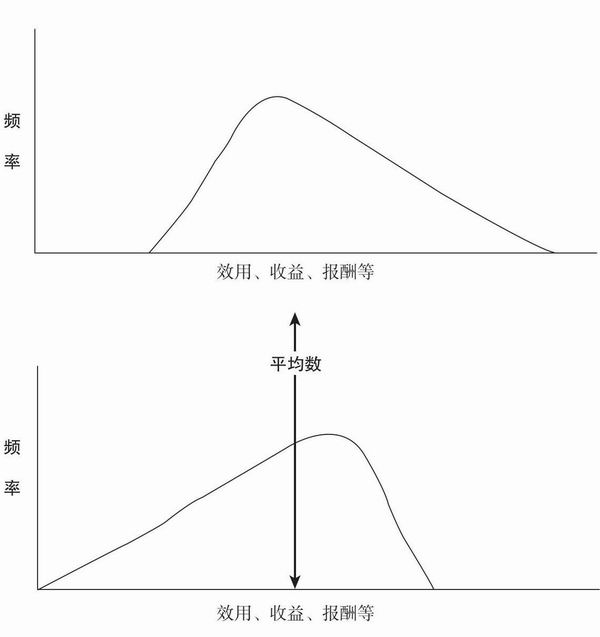
图11.6 均值和方差相同的两种偏态分布
如果图11.6代表的是某一国家收入的分布情况,那么大部分人都会非常明确地偏好上面那幅图:因为它是正偏态,曲线的每一个点都说明收入呈增加的趋势,收入的增加又提升了工作的生产力。顺便说一句,工业社会中收入的分布情况的确如此。而且,在上方的图中,最低收入的人和均值之间的差距没有下方的图那么大。下方的图中,许多人获得了高收入,但负偏态左边长尾的这部分人收入水平远低于均值。我们如果能对国家的收入进行如上的思考,那么为什么不能将其迁移到决策情境中呢?实际上,我们不喜欢选项的分布呈现很大程度的负偏态。受欢迎的彩票、赌博和竞争性比赛的结果多是正偏态(比如,赢得很多钱的概率非常的小)。不同的人在包含多种结果的赌博中对分布形态的偏好是不同的,有关赌钱的实证研究表明,包含有输赢的正偏态分布(如图11.6中第一部分所示)是最受偏好的(Lopes & Oden, 1999)。
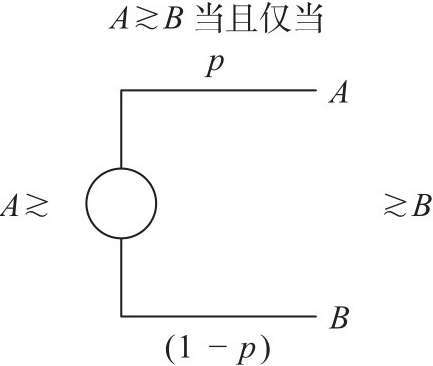
图11.7 用决策树模型描述公理6的内容
公理6.一致性:对于选项集S中的所有结果来说,用A和B代表两个不同的结果,则有当且仅当A≥(ApB)≥B时,A≥B。
公理6说明在两个选项中,如果我们更为偏好其中一个,那么只要这个选项有一定的概率出现,我们仍然会更偏好这个选项(如图11.7所示)。这条公理是无可辩驳的。
公理7.可分解性:对于选项集S中的所有结果来说,用A、B和C代表三个不同的结果,则有当ALBLC时,存在一个p值,使得B ~(ApC)。
公理7类似于Holder所阐述的物体质量中的阿基米德性质。实际上是指不存在一个选项的偏好能够绝对大或绝对小,总是存在某一种概率混合,使得两个选项的偏好程度是相同的。现在假设存在三个选项A,B,C,我们对它们的偏好顺序是ABC。依据公理描述,则存在某一个概率值将A和C混合在一起,进而使得我们对B 和AC的组合之间的偏好不存在差异(如图11.8所示)。
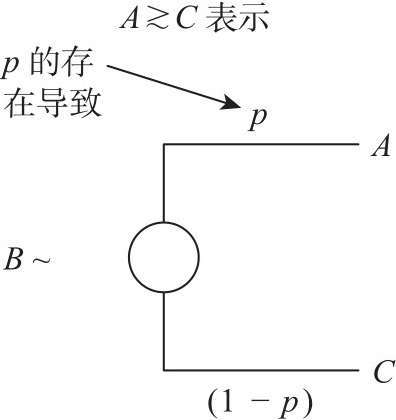
图11.8 用决策树模型描述公理7,该公理说明存在某一概率值使得我们对确定选项B和类似于赌博的选项组合AC之间的偏好不存在差异。
对于决策者来说,如果我们假设在所有的选项中,A选项具有无与伦比的吸引力,那么无论A以何种概率值出现,在ApC和B之间,都会更为偏好前者。如做适当变动,当选项C无可比拟地差于B时,同样的结论仍然成立。根据公理所述,这样的选项是不存在的。那么如果是永恒的幸福天堂或突然死亡呢?是不是一个选项只要包含了永恒幸福,无论其概率多渺茫,和其他平凡无奇的选项相比,人们就一定更偏好前者,毫无取舍的困难呢?又或者,我们其实也不会完全排斥包含一定概率死亡的选项?(或许我们不应该在这里谈论永恒幸福的话题,因为我们无法说清楚那指的是什么。)我们的行为明确地说明我们对死亡是恐惧的,并总是竭力地避免它发生,或者说我们对于生活和未来的态度是积极的。但是,我们能避开所有包含死亡可能性的选项吗?答案是否定的。我们每天的生活都充斥着死亡的风险,即便是一些微不足道的行为(如穿过马路去买报纸)。某些情况下死亡的可能性还会大于其他时候,比如坐飞机,虽然我们害怕坐飞机,但每年仍然需要依靠它飞行数千公里到外地。即使为了远离死亡而整天躺在床上不动,也可能因为长时间卧床使躯体的机能下降,从而更快地接近死亡。另外,在生活中也存在一些虽然死亡风险很大,但却是经过深思熟虑的选择,比如在战争中采取地下抵抗行动,或选择一份高薪但十分危险的职业,如深海潜水。
所有的公理看起来都十分合理。事实上,如果考虑可比性,就只有独立性公理会遭到批驳。但是,正如其他数学理论,这些公理也具有十分突出的应用价值。比如根据勾股定理,如果已知直角三角形任意两条边的边长,我们就能求出第三条边的长度。如果实际测量的结果不符合预期的话,我们通常会认为这个三角形不是直角三角形——我们几乎或从来不会说定理不正确,即三角形是直角三角形,测量也是准确的,只是这个数学推论不适用于实际。von Neumann and Morgenstern理论最苛刻的部分就是如果我们接受了该理论,就必须从期望效用的角度对不同的选项进行评价,即认为确实存在数字能够代表选项包含的每个结果的效用。(重申一下,这些数字是和只包含有一个结果且此结果出现的概率是1的选项结合在一起的。)根据可分解性公理,这些数字可由某些选择所决定,同时要求其他选择也由期望效用计算得出。而描述结果分布的其他特征变量,比如偏态,与此无关。
如果我们想设计一种方法对不同结果的效用值进行测量的话,就要用到可分解性原理。虽然本书的主要内容不涉及测量方法(详见Dawes & Smith [1985]书中的简介),但是我们可以举个简单的例子探讨一下这一基本方法。为了简便,我们现在假设只存在三个结果(可能与钱有关,但是我们还是选择一种数量性不太明显的情形):分别在A(科罗拉多州的博尔德)、B(宾夕法尼亚州的匹兹堡)和C(德克萨斯州的拉拔克)三个地方进行为期一周的旅游。进一步假设决策者对其的偏好从强到弱依次是A、B和C(依据可分解性原理得到的ALBLC的表现形式)。那么在A和C效用值中间的哪一个位置才是B的效用值呢?根据“可分解性”,我们可以赋予最受欢迎和最不受欢迎的地点的效用值分别为1.0和0.0(或者100和0,因为量表的原点和单位是随意确定的),然后向决策者展示一系列的赌博情形,直到将A和C结合起来的选项与B的效用值之间没有差别(如图11.8中的右半部分所示)。如果理论成立的话,我们就可以依据概率的组合计算出B的效用值。比如,如果决策者对在B游玩一周和有0.8的可能性在A游玩一周、0.2的可能性在C游玩的组合的偏好无差异的话,就可以认为在0~100,两端分别代表博尔德和拉拔克效用值的量表上,B的效用值位于80的位置上。这种方法可以用来在等距量表上测量任何一个结果的效用值(同时这种方法由于涉及有关偏好概率的问题,所以经常被用在应用性的决策分析问题上)。
有许多研究对效用函数,尤其是与金钱有关的效用函数进行过测量。对这种函数的分析经常被用来对个体表现出的行为进行解释和预测。比如,一条凹曲线(负增长,边际收益递减)有时说明个体倾向于规避风险,而凸曲线说明个体倾向于寻求风险。按照相关理论,这类曲线可以系统描述和预测个体在实验室模拟的赌博情境中表现出的行为,同时也适用于企业中管理人员对职业的选择。员工的职业选择在经济波动期比在经济缓和期更易表现出风险寻求的行为倾向(MacCrimmon & Wehrung, 1986;章节9.3中对效用曲线有更多讨论)。
11.4 对公理理论的传统反驳
上述理论仅描述了理想的选择情境,而并未考虑实际行为,现实是怎样的一种状况呢?von Neumann和Morgenstern的书出版后,一些理论家指出该理论不合理地限制了实际的决策行为,因此是不成立的。其中最著名的反驳是提出了两条悖论,最初这两条悖论仅从概念上进行阐述,随后得到了实证研究的证明。它们分别由诺贝尔经济学家Maurice Allais和决策理论家Daniel Ellsberg提出的(后者因泄露了“五角大楼文件”而臭名昭著,该文件主要记载的是有关越南战争的秘密内容)。
Allais悖论
Maurice Allais因论述von Neumann和Morgenstern的期望效用理论对实际行
为的限制性而获得诺贝尔经济学奖。比如,假设现在有两个选项A和B:
选项A:有100%的可能性得到100万美元(确定的选项)。
选项B:有0.10的可能性得到250万美元,0.89的可能性得到100万美元,同时有0.01的概率得不到任何东西。
当我们需要在上述两个选项中做出选择的话,大部分人都会选择A。这也就是说,如果我们遵循理论要求,就必须分别赋予100万美元、250万美元和得不到任何东西这三种结果不同的效用值,然后因为选项A的期望效用值大于B,所以我们选择了A,即:
U(100万美元)〉 0.10 U(250万美元)+ 0.89 U(100万美元)+ 0.01 U(得不到任何东西)。
根据可分解性公理,如果U(250万美元)=1.0,U(得不到任何东西)=0.0,则有0.11 U(100万美元)〉 0.10。
现在考虑另外两个不同的选项:
选项A′:有0.11的可能性得到100万美元,0.89的可能性得不到任何东西。
选项B′:有0.10的可能性得到250万美元,0.90的可能性得不到任何东西。
选项A′和B′的期望效用值分别为0.11和0.10,因为我们规定得到250万美元的效用值是1.0。因此,选择A不选择B,就意味着选择A′而不选择B′。但是,Allais认为较为合理的做法应该是在第一对选项中选择A,在第二对选项中选择B′,这也是大部分人在两种选择情形中做出的选择。为什么要在有百分之百的可能性得到一百万美元的情况下,去选择有百分之一的可能性得不到任何东西的选项呢?反之,考虑到在第二对选项中得不到任何东西的概率更大,为什么不去冒百分之一得不到任何东西的风险,而使收益扩大到2.5倍呢?
数学家Leonard(Jimmy)Savage(1954)的分析令人信服。他将不同结果的概率比作从装有100个筹码的袋子里抽出不同颜色筹码的概率,这100个筹码由1个黑色筹码、10个蓝色筹码和89个红色筹码组成。选项A就说明无论抽到哪一种颜色的筹码,都会得到100万美元的奖励;选项B说明抽到红色筹码,得到100万美元奖励,抽到蓝色筹码得到250万美元奖励,但是抽到黑色筹码得不到任何奖励。那么对于决策者来说,无论在哪种选项中,抽到红色筹码的奖励值都是一样的,选择A而非B就意味着我们更为偏好在选项A中得到100万美元的概率,而不是在选项B中得到250万美元的概率。(有时候,最终的选择可以解释为我们希望避免得不到任何东西的遗憾感:“好吧,我一开始可以非常确定地得到一百万美元,但是为了使奖励变多,我冒了个险,不幸的是事与愿违啊……”)但是在A′和B′之间选择后者,就与最初的偏好是相违背的。重申一下,在两个选项中,抽出红色筹码得到的收益都一样(不过都为0),但是现在我们更为偏好抽出蓝色筹码得到的250万美元和抽出黑色筹码得不到任何东西的结果,而非无论抽出蓝、黑筹码都得到100万美元的结果。
Savage(1954)再次通过实例对独立性公理进行了验证,同时使得这条公理更令人信服,具体内容如图11.9所示。从图中我们可以很清晰地看出,无论在哪个选项中,抽出红色筹码的概率是不变的0.89,应当与选择无关,因为每一组选项内部,抽出红色筹码的报酬相同。
Ellesberg悖论
Ellsberg(1961)主要将注意力放在赌博具有不确定性的特点上,同样对独立性原理进行了反驳。假设一个桶里有90个带颜色的球,其中红球的个数是30,黑球和黄球的总个数是60,具体各是多少未知。下面从桶中随机抽取出一个球,你更喜欢哪一个选项呢?
选项Ⅰ:抽到红球,赢得100美元;其他颜色的球,没有奖励。
选项Ⅱ:抽到黑球,得到100美元;其他颜色的球,没有奖励。
大部分人都会选择选项Ⅰ,因为我们对其描述的情形较为的确定,但是选项Ⅱ中黑球的具体个数是不确定的。
接下来给你另外一对选项,你会更喜欢哪一个呢?

图11.9 Savage对Allais悖论的分析
选项Ⅲ:抽到红球或黄球,会得到100美元;其他颜色的球,没有奖励。
选项Ⅳ:抽到黑球或黄球,会得到100美元;其他颜色的球,没有奖励。
现在大部分人都会选择选项Ⅳ,同样因为个体在具有确定性概率的风险选项(60/90)和模糊选项之间,偏好前者。(在选项Ⅲ中赢钱的概率范围是31/90~89/90。)
这种选择再一次对独立性原理进行了反驳。图11.10中的表格对上述内容进行了清晰描述。不管在哪一个选项中,抽到黄球赢得的奖励是一样的,所以最终奖励结果的不同主要依赖于抽到红球和黑球带来的奖励。但是在这两对选项中,抽到黑球和红球的奖励是一样的,按理说,具体的偏好应该不会有什么不同。但是大部分人的偏好还是出现了反转。换一种方式说,就是在第一对选项中,决策者更喜欢将赌注押在红球而非黑球上。但是在第二对选项中,正好反过来。上述的选择意味着红球比黑球出现的概率更大,非红球比非黑球出现的概率大。同时,决策者认为红球或黄球出现的概率小于黑球或黄球出现的概率,但是又觉得红球出现的概率大于黑球出现的概率。这种矛盾的推论,使得我们无法依据概率论为不同结果赋予确定的概率值。
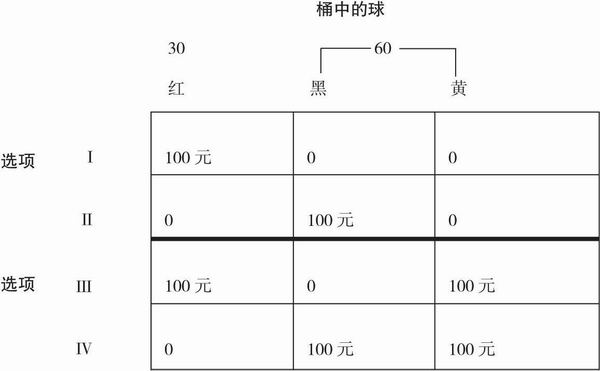
图11.10 Ellesberg悖论中涉及到的赌博情形
11.5 理论的适用条件
当然,由于某些原因,包括本书前面几章提到的决策与评价的非理性,人们并不总是按照von Neumann和Morgenstern的公理作出决策。Daniel Ellsberg ( 1961 )的评论更为经典:
有些人宣称自己是期望效用理论的绝对拥护者,他们的行为更多依据理论要求,而非直觉,对于运用“非充分推理的原则”充满怀疑。反对该理论的人可以分为三类,一类是以一种高兴的、几近狂喜的状态去批驳;一类通过分析自己的心理感受发现理论的不符之处,虽十分悲伤,但态度很坚决,拿萨缪尔森的话来说就是满足自己的偏好,让理论去服务理论本身吧;还有一类人是直觉地反对这个理论,但是却因此感到愧疚,所以就发奋图强,对该理论进行深入分析,以期有所修正。(p.655)
是不是应该做出符合公理系统的决策呢?我们的回答为带有条件的“是”,这个条件主要体现为尽管没必要被这些公理所束缚,但是在做决策的时候,还是应该考虑一些公理的内容。虽然判定某一决策是否满足公理很困难,但是当且仅当我们依据期望效用来做出选择时,公理是成立的,这提供了一种考虑其他选项的方法。比如,一对夫妻子女绕膝,选择搭乘不同的飞机达到同一目的地。这说明(根据理论)他们认为两人同时遇难要比一人遇难更为痛苦,这种痛苦程度的差异接近两倍的关系。下面我们就运用von Neumann和Morgenstern的理论对这个例子进行分析。
在这个例子中,存在着三种不同的结果:两人都遇难,其中一人遇难,两人都未遇难。因为对选项效用的赋值是任意的(针对同一问题提出的不同效用量表之间的关系是线性的),所以我们规定两人同时遇难的效用值为-1,都未遇难的效用值为0。每架飞机出事的概率都是p,且两个p值是相互独立的,所以它们同时出事的概率即为p × p或p2,这也是夫妻二人分开飞行而同时遇难的概率。但是,当他们乘坐同一架飞机,同时遇难的概率是p。接下来假设只有一人遇难的效用值为x,根据期望效用理论,则有:
p(-1)〈 2p(1-p)x+p2(-1)。
式子右半部分的第一项表示的是只有一人遇难的概率(第一架飞机失事而第二架飞机安全的概率加上第一架飞机安全而第二架飞机失事的概率)乘以x,x指的是只有一架飞机遇难的效用值,第二项表示单独飞行时两人同时遇难的概率乘以-1,-1指的是该结果的效用值。
对式子进行约分化简可以得到x〉-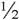 。x〉-
。x〉-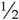 说明只有一人遇难的效用值小于两人同时遇难的效用值(负数)的一半。
说明只有一人遇难的效用值小于两人同时遇难的效用值(负数)的一半。
我们建议,应该提醒这对夫妻,他们其中一人遇难的效用值是否小于两人同时遇难的效用值的一半。在这一例子中,这可能不会改变他们的决定;事实上,上述考虑很可能会强化他们的决策。我们在这个例子中所做的就是假设人们在特定框架下,至少可以部分提高效用值,这个框架本身并不要求这种洞察力,正如在度量物体质量的物理学框架中,本身也不要求度量到的数据与我们感受到哪一个物体更重相一致。但是,正如天平度量的质量至少部分与我们对质量的感知一致,此系统内的效用值也应该与个人价值的主观感受相一致。在这两种体系中,如果没有这样的对应关系,对它们进行研究也就变得毫无意义。
下面再举一个医学方面用X射线检测肾脏囊肿或肿瘤的例子。Dennis Fryback在他的博士论文中,针对“用X射线判定肾脏病变是囊肿还是肿瘤”的问题进行了分析(具体概要见Fryback & Thornbury,1976)。标准化的程序是当病人的肾脏功能出现紊乱时,需要接受X射线检测,如果出现异常,医生应该根据X射线的结果,判断这种病变属于囊肿还是肿瘤,这种判断是概率性的,接下来病人要接受一种侵入性的检查。当时并不存在一项检查可以同时诊断出这两种可能性,而且,因为X射线结果显示的异常也可能是一种正常变化,即使其中一项检查得到阴性结果也还不能判断是否出现另一项病变,必须继续做第二项检查。Fryback研究的主题就是如何安排这两种检查的顺序,这一顺序对于病人来说是十分重要的,因为两种检查的性质迥异。
对囊肿的检测使用的是抽吸法。将针管从患者的背部插入病变部位,然后判断肾脏中的液体是否可以被抽吸上来,如果可以,则说明是囊肿。整个过程只需要局部麻醉,术后凝血的概率较小,费用较低。
对肿瘤的检测使用的是动脉造影术。先将一段软管插入患者的股动脉,然后操纵它进入肾脏,在软管末端连接的设备可以切取病变部位的组织样本,然后对获得的组织样本进行活组织检查。在Fryback的研究中,完成一次检测需要1天的术前准备,至少1天的术后住院观察。术后凝血的概率是抽吸法的10倍,同时患者感觉非常不舒服,费用较高。
Fryback发现,当医生认为囊肿出现的概率是肿瘤出现的2倍时,才要先进行抽吸法,否则就要先接受动脉造影术。他还发现,无论是患者、医生还是普通公众都认为动脉造影术的恶劣程度是抽吸法的10倍。(有趣的是,不舒适、无法工作和术后可能出现凝血是做出此种判断的主要决定因素,费用的影响作用很小——这可能是因为医疗保险的缘故,所以我们对上述两种方法在费用上的差异不是太敏感。)接下来,Fryback以动脉造影术的负效用是抽吸法的10倍为假设前提,对这两种方法进行了期望效用的分析。为了便于分析,我们先假定病人的肾脏肯定发生了病变,是囊肿或肿瘤中的一种,然后设定两种病变的概率(不过实际上第一种检查得到阴性结果后对第二种检查的要求提高了,因为病人也可以没有发生病变)。于是,我们假设在病人的异常不是正常变异的前提下,病变是肿瘤的概率是p,因此,(1-p)就是病变是囊肿的概率。同前,我们可以假设两种检测都不用接受的效用值是0,只接受抽吸法的效用值是-1,只接受动脉造影术的效用值是-10,需要接受两种检测的效用值就大约是-11。
假设放射线操作者认为放射结果是肿瘤的概率是p,如果先接受的是动脉造影术,那么整个过程的期望效用值就是
p(-10)+(1-p)(-11)式子中的第二项表示的是,在确定不是肿瘤的情况下,接受两种检测的效用值。同理,先接受抽吸术后整个过程的效用值是
(1-p)(-1)+ p(-11)那么要使先接受动脉造影术的效用值大于先接受抽吸法的效用值(即负效用会较小),即
-10p-11(1-p)〉(p-1)- 11p。
则
11p〉10或
p〉10/11
换言之,只有当病变时肿瘤的概率大于10/11,即肿瘤出现的概率是囊肿的10倍时,先接受动脉造影术才是最优的选择。回想一下,在Fryback的研究中被调查的对象认为动脉造影术带来的坏处至少是抽吸法的10倍,由此可见,10/11仅仅是个下限。但在实际情境中,当判断肿瘤出现的概率大于1/2的时候,就会选择先进行动脉造影术。
这个例子说明被调查者的个人价值与von Neumann-Morgenstern理论系统中的效用值之间至少是部分相符的。不过,人们可以对这些效用值进行评价,相信这一点看起来是相当合理的——实际上,当我们把这个结论告知医生时,他们就对检查程序做出了调整。有趣的是,把放射科医生对囊肿和肿瘤出现的概率判断与检查后实际发现的两种病变频率进行比较,会发现他们的判断非常准确,不过可惜的是,这一判断却与实际的决策完全无关——因为如果根据期望效用分析,在大多数的情况下他们应该先进行抽吸法,除非他们判断肿瘤出现的概率至少是囊肿的10倍,而这种情况是极少见的。
应用性决策分析新领域(自1970年以来)主要根据von Neumann和Morgenstern提出的方法帮助决策者优化决策(Clemen,1996;Hammond,Keeney,& Raiffa,1999)。决策分析的前提是人们确实对自己的个人价值有一定的了解,但是在某些特殊的选择情境中,尤其在决策变得自动化或必须通过特定程序才能做出时,个体价值是无法体现的。无论假设情境还是真实决策,应用性决策分析师先诱导决策者对不同结果的价值和出现的概率进行详细分析,然后通过期望效用的分析,使得决策者对不同的选项有总的看法,进而做出最终的选择。正如在医院里决定先接受哪种检测一样,这种做法意义深远。
另外还有一个例子,讲的是某小镇上一个工厂主考虑引进自动化设备的故事。他的家族拥有这个工厂已有数年,工厂为小镇上的很多人提供了工作的机会。在听了引进自动化设备可以增加利润的一个报告后,他对这一措施感到不安,但却不知原因。然后他向一位应用性决策分析师咨询,分析师通过深入了解,得出结论说他经营这家工厂的主要目的并不是赚钱,相反,他想给镇上的居民提供就业机会,以便为自己树立一定的威望。根据分析师对不同选择期望效用的分析,引进自动化设备是个非常糟糕的选择,因为这会违反这个人建立工厂的初衷。这个人听后,恍然大悟,也终于明白自己不安的真正原因是什么。实际上,在引进自动化设备可以增收的确凿证据面前犹豫不决,恰是这方面的原因。分析师的分析可以使他向自己和其他不理解他这种行为的人做出合理解释,避免决策失误。
这样的决策分析就像心理治疗,因为它帮助人们改变行为以符合自身的价值观。von Neumann和Morgenstern的理论并没有告诉我们应该做出何种选择,但却给出了解决问题的重要工具。并且,它可以帮助我们避免做出一些基本的非理性决策,因为依据此一理论框架做出的决策都是理性的。比如个体不愿放弃沉没成本,因为期望效用分析主要针对的是将来发生的事情,所以沉没成本不会进入分析过程。实际上,纠结于沉没成本的个体可以因下述理由而释怀:考虑到沉没成本会和其他经济理性行为的重要动机冲突,原先认为放弃沉没成本是浪费的动机就会消失。
决策分析师最初假设客户在特定决策情境中的态度、选择倾向与一般情境是矛盾的。分析的目的是确认,甚至是量化这种矛盾,然后希望客户可以依据自己的“基本目标”来解决问题。
11.6 关于决策分析的一些不合理质疑
因为决策分析主要通过数字和计算指导重要的决策,所以人们存在一种普遍的误解,认为这种方法缺乏感情、非人性化、令人困扰。这会不会使得一些重要的决策过程过于机械化呢,有时就像用电脑挑选橄榄球四分卫、行政总裁,甚至是情人?那些“数字”在基础学科中非常重要,但用作决策的依据,是否会变得没有意义,甚至十分荒唐呢?当人生的重要机遇是由能力测验的分数或面试官的评定分数决定的时候,难道我们还没有受够数字的奴役么?总之,人类的精神是不是能更好地体现于直觉判断,而非纠结在数字分析之中呢?
我们坚定不移地否定上述所有的质疑。在von Neumann 和 Morgenstern的理论和本书的讨论中都绝对没有想要磨灭人性或更轻易地评价并获取价值。相反,效用的提出主要是让我们掌握一种方法,在决策时判断出什么最重要。分析期望效用的目的就是帮助我们了解什么对我们来说才最重要。正如James March(1978)的观点,我们的人生目标就是要发现自己珍视的事物。这一目标可能要求我们游戏人间、恣意放纵,这种行为是不是有悖理性或期望效用理论的要求呢?绝对不是这么回事。通过观察发现,以此为目标的个体持有的是一种存在主义的价值观。决策分析的主要工作就是使这种价值观外显,使人们能清晰地知觉到自己的价值观,并调整行为以符合价值观。
决策分析也并非是令人困扰的或模棱两可的的思辩活动。实际上,一些结论可以用来指导行为而非仅仅给出想法。比如,正如之前提到的von Neumann和Morgenstern的经典之作《博弈论和经济行为》(1974),书中包含的内容要远比本书在这里所提到的内容丰富得多。书中一个十分有趣的章节介绍了扑克牌的完美玩法。一局比赛中有2 598 960种牌型,牌型之间彼此是相互独立的,为某一种牌型下注就相当于从1到2 598 960这么多数字中随机抽出一个数字,抽到数字最高的人获得此局的胜利。那么如何下注才是最好的赢钱策略呢?von Neumann和Morgenstern在这里假设只有两个玩家的一种简化牌型情境,两个玩家必须轮流下注,其中一人先下注,另一个人必须跟注(下同等的赌注)或加注(提高赌注),随后前一个人也要在此基础上继续跟注或加注。von Neumann和Morgenstern通过数学方法证明,根据期望效用最大化原则,玩家必须迅速加注至最大值,或者认输。(如果玩家是第一个下注者,他或许可以先“让牌”(check)以延迟下注,直到其他玩家有所行动。)我们想说的是,在期望效用理论的框架下,严格的数学论证表明,犹豫不决是一种糟糕的策略,最佳策略恰恰不是让人纠结于决策之中。实际上,最佳策略就是在看到牌型之前先在1到2 598 960之间选择一个数字,如果牌型的价值高于所选的数字,就赌上全部身家,否则就压根不要下注。在这个情境中,期望效用理论强调的是一种动态性的决策过程,绝对没有鼓励人们患得患失、犹豫不决或是拖延迟滞。
参考文献
Baron, J.(1988).Thinking and deciding.New York: Cambridge University Press.
Baron, J., & Spranca, M.(1997).Protected values.Organizational Behavior and Human Decision Processes, 70, 1–16.
Bentham, J.(1948).An introduction to the principles of morals and legislations.Oxford, UK: Blackwell.(Original work published 1789)
Clemen, R.T.(1996).Making hard decisions: An introduction to decision analysis (2nd ed.).Paciic Grove, CA: Duxbury Press.
Dawes, R.M., & Smith, T.L.(1985).Attitude and opinion measurement.In G.Lindzey & E.Aronson (Eds.), Handbook of social psychology (Vol.1, pp.509–566).New York: Random House.
Ellsberg, D.(1961).Risk, ambiguity, and the Savage axioms.Quarterly Journal of Economics, 75, 643–669.
Freedman, D., Pisani, R., Purves, R., & Adhikari, A.(1991).Statistics (2nd ed.).New York: Norton.
Fryback, D.G., & Thornbury, J.R.(1976).Evaluation of a computerized Bayesian model for diagnosis of renal cysts versus tumor versus normal variant from exploratory urogram information.Investigative Radiology, 11, 102–111.
Hammond, J.S., Keeney, R.L., & Raiffa, H.(1999).Smart choices: A practical guide to making better decisions.Cambridge, MA: Harvard Business School Press.
Hastie, R., & Stasser, G.(2000).Computer simulation methods in social psychology.In C.M.Judd & H.Reis (Eds.), Handbook of research methods in social psychology (pp.85–114).New York: Cambridge University Press.
Holder, O.(1901).Die Axiome der Quantitat und die Lehre vom Mass.Reports on the negotiations of the Royal Saxon Society of Sciences, Mathematics and Physics Class, 53, 1–64.
Kadane, J.B., Schervish, M.J., & Seidenfeld, T.(1999).Rethinking the foundations of statistics.Cambridge, UK: Cambridge University Press.
Lopes, L.L.(1994).Psychology and economics: Perspectives on risk, cooperation, and the marketplace.Annual Review of Psychology, 45, 197–227.
Lo pes, L.L., & Oden, G.C.(1999).The role of aspiration level in risky choice: A comparison cumulative prospect theory and SP/A theory.Journal of Mathematical Psychology, 43, 286–313.
MacCrimmon, K.R., & Wehrung, D.A.(1986).Taking risks: The management of uncertainty.New York: Free Press.
March, J.G.(1978).Bounded rationality, ambiguity, and the engineering of choice.Bell Journal of Economics, 9, 587–608.
Neumann, J.von, & Morgenstern, O.(1947).Theory of games and economic behavior (2nd ed.).Princeton, NJ: Princeton University Press.
Savage, L.J.(1954).The foundations of statistics.New York: Wiley.
Tversky, A., & Kahneman, D.(1974).Judgment under uncertainty: Heuristics and biases.Science, 185, 1124–1131.
