第3章 判断的整体框架

3.1 判断和预测的概念框架

“这场灾难不应该归咎于错误的安排，而应该归咎于所有风险中我们不得不承受的厄运……我们冒着风险，我们知道我们必须承担；总有些东西出来阻止我们，因此我们没有理由抱怨，只能向上帝的意志鞠躬，下定决心，尽最大的努力坚持到最后。”这些文字出自英国探险家罗伯特·斯科特的临终遗言。这位探险家没能寻找到南极极点，在仅离返回补给站17公里的地方，因饥饿和精疲力竭湮没在南极的冰天雪地里。斯科特意味深长的遗言把他和他的队友们描绘成了英雄——被不可战胜、变幻莫测的自然击败的英雄。但是历史似乎并不善待斯科特，如今，大多数的评论家都认为在斯科特进出南极的多次艰苦跋涉中，除了不可预测的不利事件之外，他一次又一次糟糕的判断应当对他的失败负责（Diamond，1989；Huntford，1999）。斯科特做了很多糟糕的判断，比如补给站的选址，队员、驼兽和机器的耐受力，还有探险中无数其他的细节。

本章将介绍判断的心理机制，介绍人类推理、估计和预测未知事件及其特性的能力。我们的判断能力常常会受到各种系统误差的影响，其中最突出的一个就是简单的过度自信。

人类的大脑可以超越我们的感官提供的信息，并进而超越这种“被动的提供”，成为地球上任何其他有机体的神经系统都无法媲美的“天然设计”。即便是不费吹灰之力的三维物理知觉，单靠视网膜上提供的信息，在数学上也没有办法实现（Attneave，1954；Pinker，1997）。然而进化却授予人类一套拥有特殊构造、可进行假设推理的认知系统，让我们能在三维世界里自由航行而不至于撞到大块礁石。我们的视觉系统非常擅长做一些无意识的推理，以至于我们几乎没有办法用能意识到的经验来检验我们是如何做出这些推理的。在一些脑损伤的案例中，盲视现象表明，即使因主要的视觉皮层受损而不能知觉到知觉过程本身，我们依然能做出判断。本章将要介绍的是判断的加工过程，这些加工过程让我们拥有一系列（傲人）的成就。从预期一个球的飞行路线，到内科医生通过一系列缜密的推理去判断病人的肾脏到底出了什么问题，无一不是判断的结果。

现在，我们将集中关注判断过程的心理，此处的判断特指那些以推断外部世界某些状况的本质为目标的判断（那种把判断视为衡量后果与个人价值观的内部心理活动的观点不在我们的讨论范围内）。在心理学领域，已经发展出一套专门的概念框架，用来处理事件和可能的行动路线及其结果之间的判断和预期。在今天看来，这套框架及其相关术语可能有些陈旧了，但是其中的基本概念仍然提供了一个极好的组织方案，可用来总结在不确定性无法减少的情境下的判断。不确定性无法减少，指的是在决定采取什么样的行动之前，不确定性是不能被排除的。

这个框架被称为透镜模型（Lens Model），由奥地利籍美国心理学家埃贡·布伦斯威克提出（Hammond & Stewart，2001）。我们的感官并不能与外部世界的物体和事件发生直接的联系，而只能通过介于外部物体和内部知觉之间的“透镜”来获取信息，这就是“透镜模型”名字的由来（Pepper，1942）。透镜模型分为两个部分，右半部分表示的是人们在做出判断时头脑中的心理过程，而左半部分表示的则是人们所处的真实世界中的事件和关系。这个框架提醒我们，一个完整的判断理论必须包括行为发生的环境。我们之所以称之为框架，是因为它不是一个描述判断过程细节的理论，而是借此把判断情境的各个部分装进一个概念模板之中。这一有效的模型也有助于更深入的理论分析。

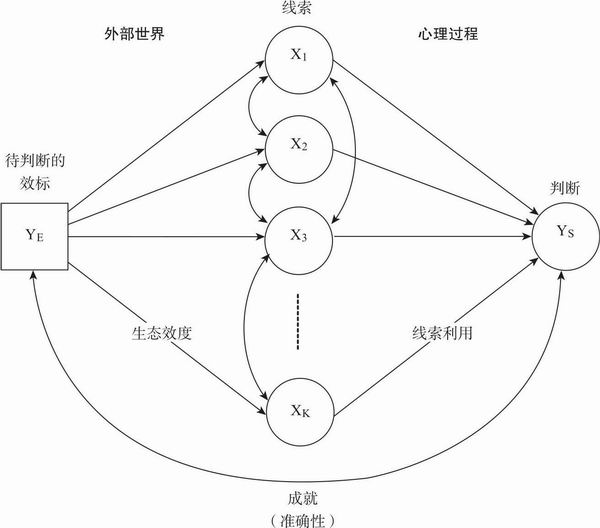
图3.1　整体判断过程的透镜模型概念框架

让我们通过概念图（图3.1），用透镜模型来分析一个判断的例子。假设我们要估计在街上遇到的某个人的生理年龄。（性别、年龄以及种族的判断通常都是自动加工的过程。）透镜模型把判断看成是一个过程。在这个过程中，我们试图通过离事物最近的透镜——也就是那些我们最容易得到的被称为线索的信息——去看清楚世界的真实状态（这个人的年龄）。在这个例子中，我们做出判断很可能是通过观察并且依据以下这些线索：头发的特征（是银白的还是秃顶的）、皮肤状况（是光滑的还是有皱纹的）、身体状况（看起来是匀称挺拔还是老态龙钟，是步态轻盈还是步履蹒跚）、他的衣着（是时髦艳丽还是保守古朴）、他的声音（是稚气未脱的、青春少年的、尖锐的、还是苍白无力），或者其他能支持年龄推断的线索。从这里我们就可以看到，就算是年龄大小这样的直觉判断，一个正在做判断的人也不能报告出来他们依据的究竟是什么样的线索。

透镜模型图的左半部分概括了所谓的效标与可能指向那些情形的线索之间的关系，效标指的是现实世界中真实的、待判断的情形，也即上例中那个男人的年龄。在年龄判断的例子中，物理人类学的研究能够阐明图表左边一列因素之间的关系：生理年龄与它自己产生的可见的线索或者符号之间真正的关系究竟是什么？在人们的概念中，这些关系通常是因果关系。要么是直接的因果关系，效标情形或者结果产生线索；要么是间接的因果关系，效标情形产生或者调节线索的价值。图中间是线索“透镜”，通过它把判断与判断的效标或者目标联系起来。连接线索（X1，X2，……）间的箭头，表示在大多数判断中线索之间存在的相互依赖关系或交互关系。图的右半部分是模型框架中判断的心理过程。它显示了人们整合线索所传达的信息，以便形成估计、预测或效标价值的判断这样一个推理过程。图中标着“成就”的拱形曲线表示判断者对待判断效标进行准确评估的能力。

用统计模型去获取一个人内部的心理“判断策略”（透镜模型的右侧部分），在读者看来或许有些奇怪，因为大家早已熟悉了外部世界中变量与变量之间常用的关系模型（透镜模型左边的部分）。为了清楚地说明统计模型在内部心理过程的应用，让我们来看一个具体的例子吧。

几年前，一些学生对本书其中一名作者（海斯蒂）在评估他的博士项目申请人时使用的判断策略非常感兴趣。每年项目组都会收到近125份申请书，海斯蒂会一一阅读这些申请材料，评价每个申请人进入项目的资格。为了研究需要，他的学生审查了每个申请文档中的内容，并把海斯蒂判断时可能依靠的28条最突出的线索赋予了量化分值。其中一些信息本身就是定量信息（比如年龄，测验分数和GPA分数），但是其他的信息大多数都是非定量的，必须经过编码。比如“大学学习质量”这个指标用四点评分量表来编码。这个评分量表是根据全美国流行的评级服务和由学生研究员主观评价出推荐信的热度编制出来的（拥有较高的评分者一致性信度）。

然后海斯蒂审查了两年来录取过程中的申请材料，并且制作出了一个评定入选资格的10点评分量表。学生们利用245份申请中28条信息和海斯蒂的10点准入资格量表，构成一个矩阵，采用统计分析的方法来确定一个最适线性模型，预测海斯蒂从这28条线索中做出的评估（参见Freedman，Pisani，and Purves，2007或者别的有关这些分析细节的统计模型）。基本上，这种方法能够粗略地估计不同信息对海斯蒂关于这245份申请做出判断会产生什么影响。虽然小心翼翼，但我们还是可以说统计模型能够总结海斯蒂做出准入判断的策略（透镜模型的右边）。在这个例子中，方程如下所示：

这个方程告诉我们海斯蒂怎样的判断习惯呢？首先，他仅仅依据四条信息——两个测验分数、推荐信和大学学习质量。第二，他显然在很大程度上依赖于标准化能力测验的分数。最显著的结果就是这个模型对海斯蒂整体行为的预测有着相当好的效果。模型的预测和海斯蒂真实评估之间相关系数是0.90。为了验证这个相关关系的正确性，海斯蒂在做完了245个申请书评测的两周之后，又找了50份申请书，重新进行了一次判断，考查海斯蒂第一轮和第二轮判断之间的相关，结果，信度为0.88。换句话说，这个模型捕获了海斯蒂在准入资格评判预测习惯中可用的每一个可靠的线索！

尽管在描述海斯蒂的行为上有着不俗的表现，但该模型并不一定能告诉我们，我们到底应该如何进行准入评估。要想做到这一点，我们就需要分析环境中各种线索与效标之间的关系，也就是透镜模型的左半部分（见Dawes，1971，一个研究生准入资格的分析）。

3.2 透镜模型框架的研究

透镜模型既然是心理学家为了研究需要提出来的，那么它就可以被看成一个用来分析判断过程的蓝图（Cooksey 1996年提供了一个很好的方法论介绍，并且综述了来自这个研究范式的结果）。一旦将判断作为研究变量，那么第一步就要确定和测量判断所依据的是哪些线索。这通常是一个很艰苦的工作，因为在所有有效的线索被发现之前，需要多轮的测量和试验。显然，对于直觉判断过程来说，这项工作就更加困难了，因为判断者根本不知道自己判断时依靠的是哪些线索。通常，专家需要做出重要决定的时候，这种状况就会出现。对于内科医生、工程师或者财务分析师来说，“分解”他们高度实践和自动化的判断过程并解释“那是如何完成的”是相当困难的。就拿年龄判断的例子来说，一开始我们可能会根据自己的直觉来判断，或许会向人请教他们是如何做判断的，或许查阅一些人体测量文献中关于老化的精确信息（一个良好的初次推测会适应性地使用科学上正确的线索来进行判断），最后形成一套初级的备选线索。然后我们会进行一个年龄判断的研究，并且保持一个开放的心态，相信在判断过程中，那套最初的线索可能需要进行调整，一直到它包含了判断过程中人们会用到的额外线索。

分析的第二步就是依据概念图的左边部分创建这个事件的模型。线性回归模型常常被用来分析效标与线索之间的关系，依据的是效标与每个可能被判断者用来推断效标的线索间的多个相关系数（参看介绍线性方程的初级统计教科书，如，Freedman，Pisani，Purves，& Adhikari，1991，或Anderson，2001）。在这种分析中，相关系数（或者是相关的统计量）表明的是效标和线索之间的相关强度（线索的生态效度）以及线索和判断之间的相关强度（通常称为线索利用系数，或者更确切的说是线索对判断的心理影响力）。尽管在很多领域，线性方程令人惊讶地、完整地概括了外部环境。模型的建造者仍会意识到，有时候线性模型也只是一个外部环境动力系统的简化或者缩影。几乎可以这么说，我们所经历的世界被近似的线性关系所主宰。

研究的第三步就要跳到图3.1的右边了。这就涉及对线索利用的心理过程建模并检验：人们是怎样利用线索对效标情境做出推断的？又一次，研究者会发现线性模型能够很好地描述这一情况。通常的研究策略是搜集待判断刺激的样本——举个例子，给被试呈现各个不同年龄段男人的录像，让其判断每个目标的年龄。此时判断者利用线索的习惯就会被代数方程所捕获，这个方程把判断和每个线索的权重联系起来（值得注意的是，这种分析的结果取决于研究者使用心理意义上的数量量表来测量线索价值的能力）。研究文献很清楚地表明，线性方程是描述线索利用过程最普遍的原理。神奇的是，不论日常的还是专业的判断，人们看上去就像是使用量表对线索进行测量、分配权重和做加减，从而推断出线索所隐含的意义。

想象一下你坐在一个医生的诊室，观察她诊断病人的过程。每个病人一进来就会先诉说自己病史，然后描述一些当前的症状。接下来医生通常会让病人去做一些实验室检查，也有可能是X光（或者是别的扫描检查）。综合了所有资料之后，医生就能做出诊断，判断出病人到底出了什么问题。把数周以来搜集到的和病症有关的资料记录下来，就可以得到这个判断任务中的线索（如病人的病史、症状和检查结果）和诊断的优良样本。或者，现在我们把情境转换到繁忙的招生办公室，想象一下考官正在审阅申请资料——对成就的客观性测量指标如测验分数、中学成绩，还有更多的像推荐信、课外活动以及个人陈述等主观性材料进行审查——然后在众多申请人中做出录取判断。同样地，你可以一直观察，直到获得了相当数量的关于线索和判断的样本为止。

用透镜模型方法分析判断，是通过代数模型计算每一个线索对某个个案的价值的总权重，从而预测判断者（内科医生或者大学招生老师）的判断。计算总权重的基础是每条线索和判断之间的线性相关系数；在其他条件都相同的情况下，相关系数越大，权重也越大。这个模型也可以扩展到非线性相关关系中（例如U型函数关系中，极端值在判断中就占据高权重——比如极度消瘦和极度肥胖的病人生病的风险较高，而适中体型的人生病的风险就要低很多；又比如一个大学招生办的老师要么喜欢参加了很多课外活动的申请者，要么喜欢专注于某一项活动的申请者，但是不会喜欢“平均的人”，即参加了2~3个活动的申请者）。这个模型也适用于基于联合线索进行判断的构型（configural）关系（比如血液中某种荷尔蒙含量处于较高水平，这对女性的身体是有害的，但是对于男性却没有什么影响；参照下面变量间“交互作用”关系的讨论）。在这里，我们又一次“令人惊讶地”成功运用了简单线性模型。之所以说惊讶，是因为很多判断者都声称他们做出判断的心理过程远比线性方程的预测要复杂得多——但事实上，线性方程却出色地“捕获”了他们的判断习惯。

如果我们掌握了判断样本的效标值，我们同样可以计算出透镜模型范式左边一栏的总括模型。然而，在现实判断任务中，很难获得效标值。在医疗情境中，要让一个医生追溯病人的病史，评估病人当前的情况并判断最终的治疗结果是件特别浪费时间的事情；类似地，在大学招生的情境里，我们也没有获取能够代表那部分未被录取的学生会在大学成功的效标值。通常我们感兴趣的是判断的心理过程，也就是透镜模型右边的一栏，而不是全部框架结构中所包含的完整的环境行为系统。

从医疗诊断到高速路安全的判定、从股票价值到牲畜质量的判断，研究者都做了成百上千的研究（Brehmer & Joyce，1988）。不同的判断领域（比如，天气预测、内科医疗、大学招生和牲畜价格的判断各不相同）和不同的判断者（不同的个体会对不同类型的线索给予不同的权重——除去少数真正出色的判断专家外，大多数所谓的专家并不比一般新手懂得更多，见Sherden，1998）其结果存在着很大的差异。冒着过分概括的风险，我们在这里大胆地总结一下专家和外行人典型的判断习惯：

1.判断者（甚至是专家）倾向于只依靠相对较少的线索（通常是3~5条）来做出判断。但也有例外，比如说在专业的天气情况判断和牲畜质量判断方面。在这些例外的领域中，判断者之所以会对更多的线索保持较高的敏感性，是因为判断者在学习如何做出判断的训练中得到了及时和准确的反馈（这与医疗诊断、招生决定或者金融预测等领域的训练不一样。这些领域里，判断者得到的通常是延时反馈或者没有反馈）。

2.只有很少的判断策略是非线性的；大多数是可加的和线性的——这与大多数判断者对自己判断过程持有的看法相反。

3.判断者对自己的判断策略缺乏洞察——他们不能准确地评估自己判断时的“线索利用权重”——尤其是专家或有着丰富经验的人。

4.很多研究（例如，学生对于外表吸引力的判断、教授对研究生院招生的判断、放射研究者对于肿瘤恶性程度的判断）表明，判断者在选择判断策略（线索利用权重的模式）时存在很大的个体差异，并且判断者在判断他们自身时，判断者之间的一致性也很低。在像医疗诊断这样重要的领域，这个结论格外令人不安，因为我们希望我们的医疗专家的诊断能和别的专家（以及生物学理论）保持一致。至少，判断者之间的不一致告诉我们，一定有人错了，这会破坏我们对所有判断的信心。

5.给判断者呈现有联系但是非诊断性的、不相关的信息时，判断者会对自己判断的准确性更自信，尽管实际上其判断准确性并没有增加。

由本研究粗略勾画出来的专家形象并不令人恭维。然而，本节的关键信息是，在对判断者的表现做出任何结论之前（要么是自觉地承认他们的睿智和准确，要么就是不分青红皂白地认为所有的判断者都无能），我们必须仔细地审查他们的表现——并且做好大吃一惊的准备。很多自大的专家揣着一堆文凭，风度似乎也着实令人钦佩，但是其判断的专业水准可能跟一个大学二年级的学生相差无几。尽管如此，也确实存在一些真正的专家，的确值得我们遵从和聘用。

3.3 在统计模型中捕获判断

历史上一些早期的心理学研究提到了一个关于判断的问题：是否受过训练的专家比由统计推导以及加权平均所计算出的结果有更高预测力。采用多元回归法分析透镜模型框架（见图3.1），我们会想到以下的问题：哪个更好？框架图左边的线性统计模型总结还是框架图右边的人类判断？大量心理学家和行为科学家研究过这个问题，他们感兴趣的是预测大学成就、违反假释条例的可能性、精神病诊断、医疗诊断、投资价值以及商业成败的结果。早期的研究中，临床专家做出推断时所依据的信息通常也被用到线性模型中。典型情况下，这些信息包括测验分数或者传记事实，但有一些研究也包含了观察者针对某些具体特性做出的评定。所有的这些变量都能够编码成与待预测的效标结果成正性或负性相关的数字（高测验分数和绩点能够预测在随后的学术工作中更好的表现；较高的白血球数预示着更严重的霍奇金淋巴瘤病症；更多的白发和皱纹表明这个人的年龄更大，等等）。

1954年，Paul Meehl出版了一本极具影响力的书，书中提到了近20个类似的研究，同样都是把人们（心理学专家和精神病专家）的临床判断与仅基于实证数据的线性统计模型的预测力做对比（即透镜模型的左边）。所有这些研究的结果中，统计方法表现出了更准确的预测力（或者两种方法打成平手）。差不多十年之后（1966），Jack Sawyer考查了45篇对比临床判断和统计模型预测力的研究。其中，没有一个研究显示临床的判断比统计预测（Sawyer把它叫做“机械性组合”）具有更准确的预测力。与Meehl不同的是，Sawyer除了考查临床和统计两种模式下基于同样信息量去做预测的研究之外，还考查了两个获取了更多信息的临床判断研究（每个被评估的人都接受了访谈），但对比的结果却显示人工判断的预测准确率较低（这些研究中还有这样一个案例，二战期间有37 500名水手接受美国海军训练，对其在训练中的表现，仅仅依靠他们的成绩或测验分数或两者结合来做预测，要比既考虑成绩和测验分数又经过判断者面试后所做出的预测更加准确）。

同样是在1954年，E.Lowell Kelly研究并探讨了非结构化面试作为一种预测技术几乎完全缺乏效度。（近年来的相关研究请参看Hunter & Hunter，1984，和Wiesner & Cronshaw，1988）。目前尚未有证据表明非结构化面试能提供除了过往行为以外的重要信息——除了能说明面试官是否喜欢来访者，这一点在某些特别的情境中很重要。（一些同学认为面试是为了避免招进“书呆子”，但是他们却不知如何在现场面试中确定一个人是书呆子，甚至，他们都不知道如何定义“书呆子”这个词。）

Lewis Goldberg（1968），一位在如何使用线性模型分析判断方面很有影响力的心理学教授，报告了心理诊断中的一个有代表性的研究。Goldberg请一些有经验的临床心理诊断师依据人格测验分数，辨别病人到底得了精神病还是神经症（诊断结果对心理治疗实践中疗法的选择和保险范围有重要意义）。他构建了一个简单的线性决策规则（把病人在三个量表上的得分加起来，然后减去病人在另外两个量表上的得分；如果结果大于45，病人得的就是精神病）。开始时用新病例为样本，以他们的出院诊断作为待预测效标值，结果，“Goldberg法则”的预测准确率达到了近70%。与此相比，人工判断的准确率刚超过随机猜测的概率（50%），最高也只到67%。所以，即便最好的人工判断也比不过机械的加减法则。

Hillel Einhorn（1972）又做了一个统计预测和临床预测的对比研究。他研究的是，在霍奇金淋巴瘤还没有治愈方法的时代（1970年代以前）如何预测患霍奇金淋巴瘤的病人的生存寿命。（Einhorn之所以对这个病感兴趣，是因为他当时刚被诊断出患有霍奇金淋巴瘤。他在1987年因此病逝世。）一个世界级的霍奇金淋巴瘤专家和他的两名助手对患者的活体组织切片的九个方面进行评估（即线索），并对每个病人病情的“严重性”进行总体评估。根据病人的死亡情况，Einhorn把专家的总体评估和病人的实际寿命做了一个相关分析。就算专家评估出来的病情不能准确到预测死亡的时间，但最起码也能够预测一个大概的趋势（至少这个专家是这样认为的）。而Einhorn发现并非如此。事实上，连这个大概的趋势都是错的：被评估为病情严重的病人反而活得更长。用专家们在评估时使用的组织切片的九个方面的特征作为数据，多元回归分析方法却在预测病人寿命上拥有更准确、更可靠的结果。

另一个惊人的例子来自于Robert Libby（1976）。他让43名银行信贷人员（其中有些人是在资产高达40亿美元的银行中就职的高级信贷人员）预测60家公司中的哪30家在未来三年里即将因为财务报表问题破产。为了方便这些信贷人员做预测，这些公司的各种财务数据（线索）都会提供给他们，比如总资产中固定资产的比率。结果，人工判断的准确率只有75%，而基于同样数据的回归分析，其准确率达到82%。事实上，仅用资产负债率一项来进行回归分析，其准确率都能达到80%。

从这些研究中我们可以得到一个经验，那就是在许多判断情境下，我们有必要向专家咨询他们会使用什么样的线索，但要让机械模型来整合线索做出判断。总体而言，线性组合模型优于人工总体判断。这个规律适用于许多不同的情境。在某些医疗和商业情境而不是心理学中，人工判断有时会显示出优越性，这是因为在这些情境中，人们多数是根据“内部信息”做出判断的，而这些信息并不适用于统计模型。如果要确保比较公平的话，就要保证专家和模型能使用相同的信息线索。一旦统计模型接收了外部信息——至少在下面的例子中——它的预测力就会略胜一筹。（比如预测重症监护室24小时内病人的存活率；参照Knaus & Wagner，1989）。Meehl后来又几次更新了他的经典结论，1996年，他和同事总结道：“对两种方法的预测准确性进行实证比较（包含136个涉及各种预测的研究），其结果表明，机械的方法几乎总是和临床方法不相上下，甚至更加优越”（Grove & Meehl，1996，p.293）。

3.4 统计模型是怎样打败人工判断的

为什么线性模型的预测要好于临床专家呢？我们可以通过以下三个假设性“原理”来解释：一个数学原理，一个“自然”原理，一个心理学原理。

数学原理是指个体变量间的单调关系和单调（顺序的）交互作用都近似于线性模型。这种交互作用呈现在图3.2中。当两个因素联合起来的效应大于这两个因素各自作用之和的时候，我们就称这两个因素存在“交互作用”：但是当一个变量和结果之间的关系方向独立于另一个变量存在时，这两个因素就没有交互作用。真正的单调交互中，高-高作用和低-低作用是不相似的，但高-高（或低低）会比用每个变量单独分析要高得多（或低得多）。如果高-高和低-低相似的话，交互作用就称为交叉，见图3.2。

举个例子，道斯的一个博士生（Glass，1967）把酗酒和非酗酒囚犯分配到轻松或者充满压力的两种不同体验中做实验。在接受心理学家对其过往经历的访谈之前，先让这些囚犯在休息室等待20分钟。在休息室中放有无醇宾治酒，实验要观察的变量是这些囚犯饮用宾治酒的量，操纵的变量是不同的体验，轻松的或者充满压力的。经历了轻松的体验后，酗酒者和非酗酒者喝了几乎一样多的量。但是在经历了压力体验后，酗酒者的饮酒量是非酗酒者的两倍（参看图3.2中间的两个图）。因此，我们就可以在压力和酗酒者的饮酒行为之间发现一个真正意义上的“单调交互作用”：饮酒量并不能被任何一个影响因素单独预测。在这个例子中，只有把酗酒和压力联合起来考虑才能有效地预测一个人的饮酒行为。然而，一项统计分析表明，这个交互作用可以近似等于两个独立的主效应：1.酗酒者会喝更多的酒；2.所有的被试在经历压力后都会喝更多的酒。只有两个主效应的情境是纯粹线性的。

为了澄清我们的数学原理，请看图3.2中的第一个。图中反映的是两个变量之间只有简单和独立的主效应：一个主效应是酗酒者会喝得更多（不管在什么情况下），另一个是在压力的情境下囚犯会喝得更多（不管是酗酒者还是非酗酒者）。线性的加权模型能很好地拟合数据。图3.2中最后一个图反映的是交叉交互作用，这是交互作用中最复杂的一种情况。在轻松的情境中，酗酒者喝得更少；但是到了压力情境中出现了反转，酗酒者喝得更多。这种情况下，线性模型就不能表示这种效应了，哪怕只是近似地。然而在实际应用中，交叉模式的因果关系是非常罕见的。所以正如我们观察到的，在非交叉的关系（更为常见的）中，线性模型几乎都能够很好地表示变量间的关系。（见图3.2第三幅图中的虚线部分。也可以参考任何一本优秀的介绍统计方法和数据分析的著作，例如Norman Anderson 2001年版的统计书就非常优秀；另外，Robert　Abelson 1995年的《统计：原则性的讨论》（Statistics as Principled Argument）也是一本见地深刻的著作，在这些书中，包含了交互作用的透彻讨论及其在行为科学中的解释和应用。）

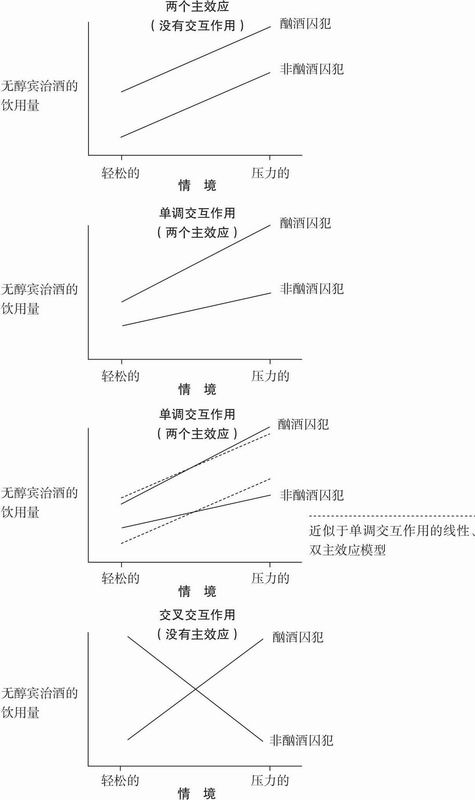
图3.2　交叉交互作用和非交叉（单调）交互作用的例子

自然原理指的是，大多数交互作用都是单调的，这个原理部分地解释了为什么统计线性模型会如此成功。对两个变量做交叉交互作用假设很容易，但要想在日常生活中发现却很难，尤其是在心理学和社会交往领域。因为某个变量取得最佳值通常都不依靠其他变量，所以大量的交互作用都是单调的。此外，虽然在社会交往领域存在一些交叉交互作用的假设（比如，独裁的领导方式在一些情境中很有效果，而自由的领导方式在另外一些情境中会有更好的效果），但最后往往发现只有口头声明和选择性的事后数据分析能验证它。事实上，Goldberg（1972）在研究教学方法与学生特点的“匹配”如何预测学生学业成就中发现，任何一种类型的交互作用都是暂时的。他在一个大样本数据集的一半中，发现了38个交互作用，而在另一半数据中只获得24个同一方向的交叉验证（同随机的19个交叉验证相比，在统计上显著差异）。

心理学原理指的是，人们很难同时注意到刺激或者情境中两个或者更多非可比的方面，这也许能解释线性模型预测为什么会成功（除“非可比性”之外，“独立可分性”和“非可比性”也是标明刺激各维度之间关系的标签）。人的注意力会在线索之间来回转移。举例来说，Roger Shepard（1964）要求被试对画着各种角度“辐条”的圆圈（刺激物就像是一个怀表的表盘一样）进行判断，被试要么只注意圆圈的大小，要么只注意辐条的角度，但不能同时注意这两个方面。评估学术申请的情形也是类似的。通常人们在判断时只会锚定一条突出的线索，比如GPA分数或者测验分数的高低，然后根据申请者的其他信息来做调整。有时，突出的锚定价值取决于信息的呈现形式，因为将某条信息（如测验分数）置于突出位置时（如申请信息表开头），偏差就产生了。信息呈现的顺序会使其具备更显著的锚定价值，从而带来判断上的误差。一些人通常是先注意到一个线索，比如有利的测验分数，随后是第二重要的线索（可能是GPA分数），然后是重要性再次之的第三线索。从以上的例子我们可以注意到，尽管锚定-调整判断策略并不那么精美，但它在认知上却非常有效地整合了数量可观的信息，以至于一定程度上可以媲美于线性模型。然而锚定-调整判断策略还不是最优的。现实中，在对申请人这一总体的分布以及申请资料库中每个学生的可预测性知之甚少的情况下，一个招生委员会的成员怎么能够理性地把测验信息和GPA信息综合起来考虑呢？作这样的比较有一个理由，即纯粹的统计模型优于总体判断。统计模型能够利用从各种线索转换过来的有效和独立的信息，把情境中的所有可得变量“校准”到标准化的范围，最后做出严谨、一致的判断。

既然单调交互作用近似于线性模型（这是一个统计事实），而现实中存在的交互作用大多数又是单调的，并且人们对来自各个方面不具有可比性的信息进行整合着实存在困难，那么线性模型胜过临床判断就是显然的。要想推翻这一说法，唯一可行的做法就是，强调受过训练的专家在整合信息方面确实优于常人（而不是他们知道应该注意哪些信息）。但是并没有证据能够表明专家就一定与一般人的思考方式不同（记得第1章中提到的国际象棋大师吗？大师并不具备特别的视觉或者智力技能，只是相对于新手来说，他们知道“往哪儿看”，在长时记忆中有更多的各种棋局知识，并且清楚在每一种棋局下应该如何应对）。

由此我们可以做一个更大胆的设想：不仅仅现实经验的世界是线性的，相应地，人类的判断习惯也是线性的。因此，线性模型不仅广泛用于描摹透镜模型右边的线索利用部分，也正确地表现了人类的思维图式（如Anderson，1996；Brehmer & Joyce，1988）。在很多基本的方面，人类的思维都遵循线性权重加法模式。事实上，我们熟知的人类大脑神经网络的工作原理也告诉我们，像大脑这样的自然“机器”，它的算法也是权重加法模式，很多基础的过程都可以很好地用线性方程来描述。我们将在下一章来探索这种判断习惯的微妙之处。

3.5 线性模型的惊人成功对实践的启示

无数的研究文献惊人一致地显示出，专家判断很少获得令人满意的准确率，几乎从未比机械判断更好。正如Meehl（1986）所说，他那本“恼人的小书”出版40年后，“在社会科学领域，一大堆各种各样的定性研究在这同一方向上得出如此一致的结论，表明在此问题上已没有争议（p.373）。”这一点对实践的启示好像也逐渐清晰：一旦有可能，人工判断就应该被简单的线性模型判断所取代。之所以说“一旦有可能”，是因为我们同样也相信，在用一种新的方法做重要的决策之前，需要做一些实证测试。我们并不提倡违背“具体问题具体分析”的原理，在所有的判断情境中都用线性模型判断替代人工判断。在现实的判断环境中总有一些特例和变化（比如发明一种新的诊断方法），需要远见和及时的调整。但是我们坚信，在专家判断上浪费的大量时间和资源，可以在统计模型中得到更公平、更有效和更准确的利用。利用人类构建的线性模型判断，比只靠人类自己判断要有效率得多。

我们提倡更广泛地使用准确的、机械的预测方法。道斯等人（1979）的研究表明，即便不使用统计上的最优权重数据，线性模型也能轻而易举地胜过专家判断。多年来，一个让道斯困扰不已的想法不断在他脑中盘旋：或许任何线性模型都能胜过专家。这种可能性看起来荒唐，但是道斯却执着于这个问题的研究。在一个助理研究员空闲的时候，道斯要求他去处理一些数据，并建立一个线性模型。要求是“除了正负号外、所有的数据都赋予一个随机的”权重（预知每条线索对效标的影响方向时，这样做是合理的）。在头100个这样的模型都胜过了人工判断之后，道斯又进行了20 000个这种“随机线性模型”的研究——其中10 000个模型的数据来源于正态分布中随机选择的一些系数，另外10 000模型的数据是从均匀分布中随机选择的一些系数。道斯用了三组数据集合：（1）根据《明尼苏达多项人格量表》的测验分数，对大约860个病人诊断其为精神病还是神经病（Goldberg“加三减二”法则中也用到过同样的数据）；（2）用招生评估的10个学术性变量和随后考查的人格特质变量数据，预测伊利诺伊州立大学心理系一年级研究生的GPA；（3）用本科GPA、GRE分数以及本科院校的入学难度，预测俄勒冈州立大学2~5年级的研究生的表现。这三组预测都同时由线性模型和专家（从研究生到优秀的临床心理学家）预测。平均来看，随机线性模型解释的效标和预测之间的方差变异是训练有素的专家基于直觉判断的1.5倍。基于数学推理，单位加权（就是把每个变量标准化，依据变化方向？ 1个标准差而引起的因变量变化）能提供更好的预测力，平均是人工判断的2.61倍。系统或随机线性模型常被诟病为不合理，是因为他们的系数（或权数）不是基于最优化预测的统计技术。然而这个研究表明，即便是如此不合理的模型，也能像那些合理的模型一样得出良好的预测结果。在解释线性模型中的系数时，系数前面的符号比具体的数字权重要重要得多。

还需要指出的是，在利用包含不同数字和单位的测量量表数据时，基于直觉的人工判断是没有竞争力的。如果一种类型的信息（如测验分数）被转换成了200到800的数值，而另外一种类型的数据（如绩点）被转换成了1到4，那么大脑很可能被愚弄，即面对大数值进行大调整。之所以举这样一个例子是为了说明，在做直觉判断时，把信息量表线索标准化是一种不错的方法。另一个有效但同样“不合理”的方法就是收集大样本的人工判断，拟合一个线性模型，用它来替代初始的判断。这个方法叫做自举引导式（bootstrapping）（不要和Efron 1988年提出的统计中的重抽样技术混淆），而且这个方法总会胜过人类专家，包括那些在原始模型中被当做“判断来源”的专家。关于自举引导式的成功有很多种解释，有人说它的信度、稳定性较好（方程不易受到不良情绪或疲劳的影响），也有人说与主观报告或者个案解释的方法相比，抽象判断策略或许能够更好地理解人们判断的真实过程。但是自举引导式成功的最大原因，可能还是要归功于它出色的稳定性和（即使是不合理的）线性模型的强大。线性模型的强大，来源于其数学性质及其与待判断环境中事件内在结构的匹配。

3.6 反对和辩驳

从上面的几个小节我们可以得出这样的结论，不论是随机的、系统的或者是自举引导式的模型，它们的预测力都普遍高于训练有素的专家。然而专家，或者是依赖这些专家做判断的人却不太乐意接受这样的事实。所有的这些发现几乎都不能对专家判断的应用造成影响。Meehl在年轻的时候就被选为美国心理学会主席，但是他的这个研究成果的实际应用却没能引起同行们的重视。拥有联邦执照的心理学家、内科医生和精神病学家做（有利可图的）总体判断时总是以这样的字眼开头：“依我之见……”。事实上，这些判断可能还比不上一个门外汉用一个可编程计算器计算出来的结果。人们对自己的总体判断没有信心，却对“专家”的总体判断深信不疑，这种强大的信念瓦解了一系列优良研究发现的价值，并且主宰着我们的法律和医疗系统。

人们反对这种准确的统计判断模型有很多原因。首先，它公然冒犯了很多专家的自恋情结（同时还威胁到他们的收入）。捍卫专家判断的一种常见方式是，对在特定研究中做总体判断时用到的专家的专业知识提出质疑。一位密歇根大学的心理学教授常常会嗤之以鼻地说：“哼，对方只不过是明尼苏达的一名临床医生而已！”殊不知，大多数明尼苏达的临床医生都是在密歇根大学拿到博士学位的。“你们用过X博士的判断吗？”，一所很有名望的医学院院长告诉我们说，“他的判断一定与病人的实际寿命有关。”事实上，X博士正是Einhorn在霍奇金淋巴瘤研究中的一名被试。

另一些反对线性模型的人坚持认为，线性模型只在一些短暂的和琐碎的事情上有更好的预测效果（比如死亡时间、出狱时间或者是退学）。他们声称，在“真正重要的长期结果预测”中，总体判断有着更好的预测结果。但是Jay Russo（在私下交流中）指出，这个反对的理由只能说明长期预测比短期预测更容易。像预测死亡（100年以后我们都会死去）和狂犬病（在潜伏期之后就会发病）这样的变量是可能的，但是这些变量并不是这些研究中要预测的那类变量。还有，如果我们了解一下过程（比如血液中存在狂犬病病毒或者艾滋病病毒），预测“潜伏周期”就变得像演讲中提到的某个数字一样不重要了，同样地，预测长寿比预测死亡更容易。

最后一项反对的理由就是，“不可能所有的人都错。”专家们因为他们“依我之见”的判断被人们敬畏了很多年，同时也获得了很丰厚的报酬。然而就像James March所说的，这种敬畏可能只起到了社会作用。老百姓和相关组织常常只需要在好坏参半的备选选项中做出选择。所以判断一个决策的好坏，咨询专家就成了一个标准，而且这个专家收费越高越好。“我们已经尽最大的努力去获取可能最好的医疗建议了，”这种想法可能是一场致命手术（或者输掉的官司）的安慰剂。就像丢掉《易经》就能使某些人免除对失败婚姻或者一个错误职业选择的悔恨。构建线性模型的专家给人的印象，根本比不上依靠“多年经验”的直觉“顿悟”而进行判断的专家。（据我们所知，一个收费很高的咨询专家在私下里偷偷地使用线性模型。）所以我们对专家判断价值的评判是独立于其效度的。

除此之外，还存在一种环境因素让我们不相信总体性直觉判断存在劣势。那就是反馈的可得性是有偏的。在一个预测情境中构建线性模型时，我们能够准确地知道这种方法的不足。但相反的是，我们对于直觉判断的反馈是有问题的。我们不仅选择性地只记住了成功的时候，还常常意识不到自己的失败——因为我们用已有的知识把它们“解释掉了”。谁知道被研究生院拒绝的申请人现状如何？教授只能接触到录取的学生，如果某个教授的工作成绩优异，被录取的学生同样可能会表现得很好，这就会强化教授对自己的判断效果的信心。但是被误诊为“精神病”的患者呢？如果幸运，他们将在诊断他们的权威人士眼前消失；如果不幸，他们有可能被安排到很快就会使其变成精神病的环境中。最后，病人因接受不了而自杀，医生会解释说：这是因为该病人送过来时的情况已非常严重了，以至于他们还没开始治疗就发生了悲剧。不相信？你可以去查看病历，所有的情况都记载在他的病历里。

有关反馈的问题在Malcolm Gladwell的畅销书《当机立断：不假思索的思考力量》（2005）中有举例解释。Gladwell讲述的故事是关于盖蒂博物馆中一尊所谓公元前4世纪古希腊创作的、名为“科诺斯[1]”的年轻男性裸体大理石雕塑。这尊雕塑的来源并不确定，所以博物馆就请了专家，用科学方法来确定石头和它表面的材料成分是否和真正的古希腊雕塑相同。专家给了肯定的结论，博物馆也跟着把它买了下来。然而当雕像展出的时候，一些艺术历史学家看到这尊雕像的第一眼时便倒吸了一口凉气。希腊一间有名望的博物馆主管Angelos Delivorrias说，他感觉到了一阵“直觉上的厌恶”。当时世界上最有名的博物馆馆长Thomas Hoving（1996）说，他看到雕像的第一个感觉就是太“新”了，并且评论道：“在西西里岛挖掘的时候，我们也发现了一些类似的零零碎碎的东西。只是没有这么成型（p.315）。”（然而值得注意的是，这尊雕塑到底是真的还是高仿品至今仍然存在争议；Goulandris Foundation & J.Paul Getty Museum，1993）。

从上面这个表面上直觉判断胜过系统分析的例子，我们能得到什么样的结论呢？第一，在检测这个领域的造假上，化学检测可能不是最好的方法。如果这尊雕塑真的是赝品，那么造假者肯定对何时选择大理石材料和如何“做旧”做了很多研究。但如果没有做过前景性研究（就像那些进行评价线性模型的例子），我们不知道在这事件上拥有正确直觉的专家，在其他伪造品的判断上有多少次正确。谁知道他们以前被愚弄了多少次？我们甚至不知道，就在这个雕像的真伪判断中，有多少其他专家的直觉是错误的。这就像我们举的一个例子，有36个人预感掷骰子的下一轮会出现两点，并且愿意在成败机会相当的情形下赌上一把，结果平均只有1个人会赢。赢的那个人引起我们的注意，而另外35个可能都不怎么被提及。

另一个有启发性的例子是“亲爱的阿比”提供的1975年时的一封信：

亲爱的阿比：在一个高级杂货店排队结账时，我看到一个在我正前方的女人在疯狂地翻找她的钱包，很尴尬的样子。看起来她的东西已经结算了，但她还差一美元。我很同情她，就把一美元递给了她。她很感激我并坚持要了我的名字和地址，写在一张皱皱巴巴的纸上，然后放进她的钱包里，说：“我明天一定把钱邮寄给你。”然而几个星期过去了，我仍然没有收到她的来信！阿比，我认为我对判断人很在行，而且我并不想认定她是那样的一个人。这点小钱一点也不重要，但是这却动摇了我对人的信心和看法。希望得到你的看法。