第7章 偶然与因果

7.1 对偶然性的误解

1972年1月26日，22岁的南斯拉夫空服人员维斯娜·瓦洛维奇正在南斯拉夫航空JAT 367次航班上为乘客们提供饮料。不料，一个克罗地亚的民族主义恐怖组织在这架飞机上装了一颗炸弹，炸毁了飞机。大多数人会觉得她倒霉透了——首先，她工作的航班遭到了这样一次罕见的袭击就够倒霉了，更倒霉的是，她本来不该在这次航班上工作，但安排工作时搞错了她的名字，因此这对她来说完全是一次阴差阳错的飞行。不过这个故事也有好的一面：瓦洛维奇小姐奇迹般地生还了，她现在还保持着不带降落伞从高处坠落生还的世界纪录——33 000英尺 （10 000米）。而此次飞机失事后仅仅过了一年多，她就宣布已经做好重返工作岗位的准备，她将自己描述为一个“乐观主义者”，为上帝怀有新的信仰。这么一来，许多人又会认为她是一个千载难逢的幸运儿。不过瓦洛维奇小姐自己却比较赞同人们对她的第一个评价：“我并不幸运，每个人都认为我是幸运的，但他们弄错了。如果我真的幸运，就根本不会遇上这样的事故”（Bilefsky，2008）。

人们在思考和讨论一些非同寻常的事件时，常常会有截然不同甚至有时完全相反的观点。这并不奇怪，毕竟这些事件往往都神秘莫测，人们对其知之甚少。但即使撇开这一点不谈，我们大脑本身的设计似乎也不太善于对偶然性和不确定性进行系统的推理。可能是因为一些演化上的原因，我们倾向于对不确定的事件进行过度解释，而且，即便明白这些事件本质上就是无法预测的，我们还是会对事件的经过产生奇异的想法，其中包括许多迷信的观念（Sagan，1997）。正因为我们对不确定性和随机事件有一些与生俱来的错误观念，因此，只要对概率论这样一个技术框架略知一二，我们看待世界的方式就会发生巨大的变化。但是，如果没有特别的训练，没人会以概率的方式看待世界。相反，在人们看来，整个世界中的各种事件和事物看起来都像是由因果关系粘合在一起的，并且大多数人确信这些因果关系是存在的，他们在思考的时候关注的是因果关系的强度，而非概率。

我们一直以来都尽量注意不将世界说成是概率的或随机的。概率论是一种用以描述世界的语言，更准确地说，描述的是我们关于这个世界的信念之间的关系。对大多数人来说，这是一种不太熟悉的语言，有一堆特殊的符号性词汇和语法规则（概率论的简介参见附录）。就像我们前面所说的，一直到近代的西方文明史中，概率论才开始出现，而“概率”（probability）这样的词汇直到17世纪才进入英语词典。[词典编撰者认为“可能”（probable）这个词是从“认可”（approvable）这个词中提取出来的，比如，一个“可能”的丈夫最初是指一个可以接受或者在道德上获得“认可”的丈夫。]

有的时候，我们确实会在日常生活中谈论到偶然性、运气、概率或随机性这样的词汇——我们说“她运气真好”，“这件事是偶然发生的”，“那是一个随机事件”。但是对这些说法最到位的解读则是：这些话反映了说话人头脑里的知识状态。哲学家庞加莱（1914/1952）在一篇睿智的文章中探讨了偶然性的本质。他认为，日常生活中我们所提到的事件都是由确定的物理过程所引发的，而有些特别的事件之所以会被说成是随机、偶然性或概率性的，是因为这些事件的因果关系比较隐蔽或复杂，还不为人所知。回到本章开头的故事，我们说不清楚到底发生了什么样的物理事件而让维斯娜·瓦洛维奇与死神擦肩而过，但是我们相信，她得以幸存的原因，所涉及的一些物理条件是可以具体阐释清楚的——只要有足够的信息。如果我们当时能够对她的坠落过程进行观察，包括在那一瞬间她是如何接触地面的，以及接触前最后一刻她身体内部的状态，我们应该就可以从物理因果关系的角度来解释这次载入史册的死里逃生。

再举一个例子，我们把抛硬币看成一个随机过程，并且把“正面”事件（理想）的概率值定为0.50，但实际上我们却相信，抛出一枚硬币会得到什么结果，其背后隐藏的所有生物和物理事件都是确定的。事实上，手法娴熟的魔术师（如数学家戴康尼斯）已经发展出了一些技巧，能够对抛硬币这个看起来明显不可控的过程进行控制，并准确无误地抛出他们想要的正面或反面的结果（Bayer & Diaconis，1992；Diaconis，Holmes，& Montgomery，2007）。当然，物理分析也有不同的水平，比如，如果在量子水平上进行分析，科学家们所讨论的因果关系就不会直接对应于我们所体验到的那些机械原理下的因果关系，不过我们并不是在量子水平上体验世界，所以探讨那些事件的时候很少会这么来讨论。

当然，在我们周围的环境中，某些部分是与理论随机过程（theoretical random processes）中的理想行为非常接近的——那些在赌场或彩票中的事件看起来是由确定的物理过程所“引发”的，但是其中的因果机制太过复杂，事件的决定因素太过微妙，因而最好是在概率论的框架下来考虑这些情境。本书最重要的一个信息就是，对于所有不确定情境中的判断，我们都应该用概率论来组织思维，哪怕我们对其中某些情况的因果机制比对赌场的了解更多（或更少）。不过，即使在一些我们知道是由偶然性决定的琐碎小事上，我们还是倾向于否认这些事件里存在随机的成分。有一个有趣的故事，说的是一位西班牙全国彩票中奖者，当采访他有什么秘诀时，他说他有意选择了一张尾数为4、8的彩票，他解释道：“我连着7个晚上梦见了数字7，而7乘以7等于48”（Meisler，1977）。

7.2 控制的错觉

在一系列巧妙的实验中，哈佛大学的Ellen Langer（1975）证明，我们常常会自然而然、无意识地将偶然的事件看做与技巧有关，从而认为它们是可控的，比如赌徒们想要掷出一个较大的数字时会更用力地掷骰子。Langer设计了一种彩票，每个被试会获得一张卡片，上面有一个美国橄榄球联盟的球员名字和照片，另外有一张相同的卡片会放在一个袋子里，如果被试从袋子中摸出的卡片与自己拿到的那张相同，就能赢得彩票。这个实验分为两种条件，其中一组被试可以自行选择要哪个球员的卡片，另一组被试则由实验者来分配卡片，显然，无论被试能否自由选择卡片上的球员，他们赢得彩票的概率都不会受到影响，因为袋子里的卡片是随机抽取的。然而，当实验者向被试提出要购买他们的卡片时，那些自己选择卡片的被试所开的价钱平均是那些随机分配卡片的被试的4倍之多。在被试接受询问的时候，没有人提到自由选择球员会影响到他们赢得彩票的概率，但他们的行为却好像在说这种影响是存在的。

在另一个令人震惊的实验中，Langer和Susan Roth（1975）能够让耶鲁大学的本科生相信他们对抛硬币结果的预测能力是在平均水平之上或之下。这是如何做到的呢？在实验中，被试会得到一个虚假的反馈，知道自己的表现与机遇水平差不多——猜30次对了15次。但是实验者操纵了被试在30次猜测中是前面对得多还是后面对得多。实验结果与首因效应（primacy effect）[或锚定和调整（不足）效应]相符，前面对得多的被试倾向于认为他们在预测方面是“在平均水平之上”的，而后面对得多的被试则判断自己比较差。（显然，由于随机波动的缘故，在30次那么少的情况下，预测抛硬币结果的成功概率是不可能保持不变的。）此外，“超过25%的被试报告自己的预测表现会受到分心物的干扰，而40%的被试认为预测表现可以通过练习来提高。”因此，人们不仅在行为上会表现得他们好像可以控制随机事件，也直接表达出他们有意识的想法，认为这样的控制是一种能力，和其他能力一样，会受到分心物的干扰，还可以“熟能生巧”。重要的是，要知道这些被试都来自于世界上顶尖的大学，但是他们仍然认为预测抛硬币的结果是涉及某种能力的，而非纯属运气。

此外，就像心理学的大多数日常应用一样，赌场和彩票经理这样的从业者对于这些原则已经有了一些直觉性的了解。许多有关概率的商业博弈常常会包含一些欺骗性的技巧元素，这些有意设计出来的元素，用以迷惑玩家，使他们误以为自己在这些博弈中可以有控制的能力和机会。在许多国家，彩票玩家可以自行选择下注数字，而在彩票中也常常会有一些广告语，令玩家相信彩票是与能力相关的：“打出全垒打，赢得大联盟奖金”、“只要买个保龄球，你就能成为赢家。”

控制错觉还会导致一个更为严重的后果，那就是我们更偏爱开车而非坐飞机。这个（从生存角度来说）非理性的习惯，至少部分原因是因为我们认为开车相比坐飞机“更有控制感”。实际上，在一次越洋飞行中丧生的概率与开车20公里丧生的概率大致相等——许多时候，只要你到达了机场，就意味着旅行中最危险的部分已经结束了（Sivak & Flannagan，2003）。根据Gerd Gigerenzer（2006）的估计，在“9·11”恐怖袭击事件中，除了3 000名直接受害者之外，其后由乘飞机改而选择开车的转变，额外导致了1 500人死亡。

控制错觉研究中最有趣的研究之一表明，在现实世界的投资情境中，控制错觉与随后的不佳表现存在联系。四名英国金融学专家请四家投资银行的交易员玩一个计算机游戏，在这个游戏中，游戏者试图去影响一个虚拟的投资指数（Fenton-O’Creevy，Nicholson，Sloane，& Willman，2003）。实际上，指数的变动完全独立于这些交易员的行动——指数是随机的，有一个微弱的增长趋势。这些交易员进行了四轮游戏，然后对自己在拉升指数方面所做的贡献进行评估——因为指数的变动与交易员的行为无关，因此这个问题测量的是个体的控制错觉。平均来看，交易员们都陷入了这样的错觉中，他们均认为自己确实影响到了指数的变动。更为有趣的是，交易员的控制错觉水平与其收益以及上司对其才能和绩效的评价呈负相关。控制错觉程度更强的交易员的收益大大少于那些更切实际的交易员（差异金额在10万美元的量级上），对所在银行的利润贡献更少，上司对他们在风险管理、分析能力和人际技能方面的评价也更低。

7.3 看到并不存在的因果结构

代表性和基于情景的思维导致的恶果就是使我们看到一些并不存在的因果关系或结构（即非随机性）。这是因为，我们对于随机性的朴素概念中包含了过多的变化，于是，哪怕某个过程代表了一个理想的随机试验，我们对随机性的错误概念也往往会让我们认为这个过程不是随机的。让我们考虑一个再简单也再熟悉不过的随机过程——抛硬币，如果要求人们“表现得像一枚硬币”，自行生成一个序列，包含正面反面的抛硬币结果，这个序列要反映出一枚“公平”硬币（这里的“公平”是指抛出正反面的概率相等且多次抛掷结果互相独立，详见附录A.2。——译者注）所抛出来的典型结果，那么大部分人所生成的序列中都会包含过多的交替——非随机性地出现过多的正面-反面和反面-正面的变换。[在不同的结果序列中选出“真实硬币”的任务中，人们也表现出了同样的偏差（Lopes，1982）。]代表性之所以在其中产生影响，是因为当我们需要对随机和非随机的事件“发生器”进行区分时，会依赖于我们对随机过程的刻板印象（就和我们对女权主义者、银行职员或艺术史专业学生的刻板印象一样），采用相似性来判断或生成一个序列。因此，当我们遇到一个真正随机的序列时，就很容易会因为它看起来不够随意杂乱（因为它出现的交替少于我们对一个随机序列的错误刻板印象）而断定它是非随机的。

假设你用一枚公平的硬币（从你自己的口袋里拿出来的）来玩Langer和Roth（1975）的抛硬币游戏。抛了8次之后，你尝试要预测下一个结果是正面还是反面。值得注意的是，之前硬币每次都是得到正面，一连8次正面。如果你和大多数人一样，那么你会感觉第9次出现反面的可能性更大（你感觉“应该这样”），甚至可能会下点赌注在反面上。这种感觉还有一个例子，我们常常会看到这样一个并不正确的赌博建议：“在拉斯维加斯，如果你看到一个轮盘赌连着3次以上都停在红色，那就押黑色，稳赢。”人们对这样的说法甚至可以讲出其原理：连续9次正面（或红色）的情况非常少见，几率显示这几乎不可能发生[对硬币来说是（1/2）9，即1/512或大约0.002的概率，轮盘的概率则更小]，因此如果你连续8次出现某一面，那么连续9次出现可能性会很小。这样的直觉和推理称为赌徒谬误（gambler’s fallacy）——这种观念认为，如果一个（独立随机的）事件有一段时间没有发生，那么就该说“这个事件发生的时机已经成熟了”。硬币和轮盘都没有记忆，在一个序列中每次事件发生的几率都与其他所有事件互相独立，因此出现反面或红色的概率是恒定的。

许多人都相信空难是接二连三“扎堆”发生的——祸不单行。[笔者认识的一位临床心理学家将这样的巧合作为“荣格共时性”（Jungian synchronicity）的证据。]Russell Vaught和Dawes从美国联邦航空局那里获得了1950年至1970年各家航空公司空难的所有数据，对空难发生的间隔天数进行了考察。一个完全随机的模型假定，在任意一天发生空难的概率是恒定的p，于是从某次空难发生之后算起，考察第二次空难发生的概率。在紧接着的第一天发生第二次空难的概率为p，而在第二天发生第二次空难的概率则为（1-p）p，因为紧接着的第一天必定是没有发生空难，随后在第二天发生空难。[请注意（1-p）p小于p，这个结果对一些人来说是与直觉相反的，也许可以类比第5章中“女权主义的银行职员琳达”。]以此类推，第二次空难发生在第一次空难后第三天的概率为（1-p）（1-p）p = （1-p）2 p，第二次空难发生在第n天的概率为（1-p）n-1 p。

Vaught和Dawes（未发表研究）对所有的空难和所有毁灭性的坠机事件分别进行了考察，发现基于p值恒定的随机理论模型的拟合程度接近完美。那么空难看起来会“扎堆”发生，这是为什么呢？因为当j〈k时，（1-p）jp〉（1-p）kp，所以真正的随机序列确实包含了事件的“扎堆”。问题在于代表性思维会引导我们断定这样的随机模式是非随机的，相反，我们会假设出一些诸如“势头”这样的正反馈机制来进行解释（采纳“荣格共时性”假设的人是少数）。举例来说，虽然像“乐极生悲，否极泰来”这样的箴言可能是对的，但是我们也能找到一些反驳证据，在那些成功概率很高的人或组织身上我们会发现连续成功的模式，或在那些失败概率很高的人或组织身上看到连续的失败——哪怕这样的模式来自于独立事件。

有一个情境，人们在其中清楚看到的模式在数据中并不存在，这就是篮球比赛中的热手现象（hot hand phenomenon）。热手并不纯粹是指有些球员的投篮比其他球员更为精准，而是指一种（人们假设出来的）正反馈表现过程，即球员在得分后更容易得分，失分后接着失分。（请注意，同样的词语“热手”也用来形容成功的骰子赌徒，尽管根据一般的常识，我们都知道在正常运行的游戏中，赌徒们无法控制骰子滚动的结果。）Tom Gilovich、Robert Vallone和Amos Tversky（1985）以实验证明了热手效应并不存在，对一个球员来说，某次投篮命中之后紧接着投篮再命中和投篮不中的可能性差不多。至少，无论是费城76人队的原地投篮、波士顿凯尔特人队的罚球，还是作为实验控制组的康奈尔大学校篮球男女队的原地投篮，都没有发现有关热手效应的证据。但是，球员对自己投篮命中与否的预测则出现了热手效应，即便他们的实际表现并不存在这样的效应。一个球员之前刚刚投进2到3个球后再次投球，其成功率是不是会高于之前没投中2到3个球的时候？在一个针对一群篮球运动员和体育记者的调查中，90%以上的人回答“是”。

Jay Koehler和Caryn Conley（2003）在以往研究的基础上，分析了美国职业篮球比赛4年远投大赛的情况，从中寻找非随机的模式。在这个比赛中，NBA中投篮命中率最高的投手们要在60秒的时间限制内在三分线外（从球场的这个区域投篮命中可得3分而非2分）尽可能获得高分。这个研究同样没有发现有任何非随机的证据。即使研究者在分析中特别考虑了转播解说员所提到的“热手”，也还是没有出现这样的模式。值得注意的是，在其他一些诸如保龄球、射箭、台球和高尔夫这样的运动中，一些非随机的连胜或连败得到了证实，这说明如果在数据中确实存在这样的模式，统计分析足以敏感地将其捕捉到的。（这里看起来似乎存在一个更大的假设：在非互动的、均匀场地的运动中，球员的表现中会出现一些微妙的序列效应；而在无序的、球员之间正面接触的互动型运动中，就不存在这样的模式。）

这些研究并没有证明篮球比赛中热手效应的普遍不存在性（如果你考虑这个问题，你觉得证明存在和证明不存在哪个更困难？），不过这些结果暗示我们，如果热手效应存在，这个效应也是很小、很罕见、很不可靠的。要说任意一组具体的数据都是随机的，未免牵强，因此比较站得住脚的说法是，生成这批数据的过程是随机的，也就是说，数据的观察者无法获得必要的信息来对数据中的事件进行任何程度的具体预测——对观察者来说，概率或随机过程就是对这批数据的最佳描述。热手效应这个例子会让人备感惊讶，因为对人们来说，这样一个因果过程似乎很容易就能想象出来，能够产生预期（可惜观察不到）的模式。举例来说，有一个对Gilovich等人（1985）和Tversky和Gilovich（1989）的观点的回应，认为他们没有发现隐藏在数据中的真实的热手效应模式，其原因在于他们忽略了得分的时机。Patrick Larkey、Richard Smith和Jay Kadane（1989）发表了一篇重新分析这些研究数据的文章，其中的数据只包含那些在时间相距很近的情况下的连续得分。他们发现有一个球员，底特律活塞队的“微波炉”文尼·约翰逊，他的表现偏离了随机模型，“微波炉”这个绰号正是来源于他连续得分的名声。然而，Gilovich等人（1985）在反驳中指出，重新分析数据只发现了一个“热”球员，并且他的连续得分情况之所以在统计上达到显著，完全是依靠了一个连续7次得分的情况。随后他们进一步指出，回顾原始的比赛录像，并没有发现连续得分7次的情况，事实上，那一次是“微波炉”连续得分4次，然后在1次投篮未中后抢下篮板补中，之后又得分1次。纠正了这个数据收集上的错误后，连“微波炉”也没有偏离随机模型。

如果有一个病人连续3周情况良好，是否就意味着针对他的疗法是成功的？连续3周情况不良是否意味着失败（或者乐观一点说是“开始出现问题”）呢？球队连输3场是否意味着教练要下课？某公司连续3个季度业绩下滑是否就意味着CEO要下岗？不，抛硬币的时候区区3次连续正面并不能说明这个硬币是被人动了手脚的。然而，了解某个人成功与否的基础率（尤其在这几个星期或季度的表现之间完全无关的时候还要去预期比实际更多的交替变化），使得人们极有可能去推测在这样的连续中存在因果因素，尤其是一些与行动者自身行为存在关联的因素。[还有一个解释的角度：在日常表现中，我们比较容易看到的那些“热”或“冷”模式，其关键因素是不是在这些情况下“连续”击中或漏过具有知觉突显性？在球迷们热烈讨论“热手”的那些职业篮球比赛中，投篮命中的成功率大大高于50%，因此，连续“命中”会比较寻常，从而与我们所预期的较多转换（命中未中和未中-命中转换）相违背。如果换作是在棒球击打中，球迷谈论更多的是“低谷”，因为棒球平均击球成功率远远低于50%，所以连续“漏击”就会变得更为明显。]

为什么我们会期望有过多的交替变化？Tversky和Kahneman（1974）将这种预期归因于我们的错误信念，即认为哪怕是很小的序列也必须要能代表总体，也就是说，我们框出来的很小一部分事件的比例也必须匹配（或代表）总体中的比例。举例来说，抛硬币的时候，我们知道可能序列的总体中正面数量应占50%，因此我们会预期在一个抛4次的样本中，也是有50%的正面。当每次抛掷互相独立的时候，就会比实际情况需要更多的交替。（极端情况下，2次抛掷的序列中如果要50%的正面，则需要每次正面都是接在一个反面之后，反过来亦是如此。）在这里，代表性思维使我们从对模式的关注变成对特征的关注，而不是从特征到模式。然而，无论是特征还是模式，这种基本的信念同样都源于相似性匹配，也就是联系。此外，这个效应也会受到我们相对狭窄的注意广度的影响——我们希望自己能记住或想象的较短序列是具有代表性的。

考虑下面Tversky和Kahneman（1974）的研究中的一个问题：

有调查访问了一个城市中所有生育6个孩子的家庭。在其中的72个家庭中，男孩和女孩的实际出生顺序是“女男女男男女”。那么根据你的估计，实际出生顺序为“男女男男男男”的家庭数量为多少？实际出生顺序为“男男男女女女”的家庭数量又为多少？

几乎每个人（80%以上的回答者）都判断后面两个序列比第一个序列的可能性要小。然而，所有实际序列都具有相同的可能性（任意实际序列的概率都为0.5×0.5×0.5×0.5×0.5×0.5，即0.015625，差不多相当于在1 000个生育6个孩子的家庭中每种序列上会有16个家庭。）为什么人们会有一种很强烈的直觉认为“女男女男男女”的情况更多？因为这个短序列捕捉了我们关于随机过程的所有直觉：这个序列表现出正确的比例（一半男孩，一半女孩），并且看起来是随意的，有许多交替的情况——一句话，这个序列看起来“确实很随机”。（这种序列也和我们对于一个普通篮球运动员的命中失误情况的预期差不多，即命中和失误并没有很长的连续性而是不断地交替变换，因此当我们看到一个球员的表现有许多连续的命中时，我们会倾向于说：“这不可能是随机的，这个球员绝对是‘打热了’。”）与之相反，第二个序列看起来可能性就不那么高了，因为它的出生比例不对（男孩太多），违反了小数定律，而第三个序列虽然比例上没问题，但是看起来太整齐了（连续3个男孩，然后连续3个女孩）。

有时候，这种对于随机序列交替的信念（因为上6次轮盘赌结果都为黑色，所以确信“红色应该来了”这样的赌徒谬误）会走向一种荒唐的极端。举例来说，请看下面“亲爱的阿比”这封信的开头：

亲爱的阿比：我和丈夫刚刚有了我们的第八个孩子，又是一个女孩，我现在真的非常失望。我的小女儿很健康，我想我应该感谢上帝，但是阿比，这个孩子应该是个男孩，医生也告诉我说，根据平均律，这次我们心想事成的可能性是100比1。

人们倾向于看到或推断出一些完全不存在的模式（或因果关系），第二次世界大战中德国V-1和V-2导弹轰炸伦敦的事件就是一个很“形象”的例子。伦敦报纸刊登了轰炸地点的地图（见图7.1），市民们立刻就看出了一些集中打击的地点，并且将这些信息作为参考来解释敌军的意图。他们是如何来解释自己所看到的这些模式的呢？英国市民们推论，他们所看到的打击模式反映出敌军有意避开某些区域，而这些区域正是德国间谍的藏身之处。然而，古典概率模型分析的结果证明，这些打击地点与一个随机泊松过程生成装置所模拟的结果是完全一致的，也就是说，没有任何理由能推断在这个模式背后存在着一个系统性的动机或因果关系（有关的数学分析参见William Feller经典的教科书《概率论及其应用》）。

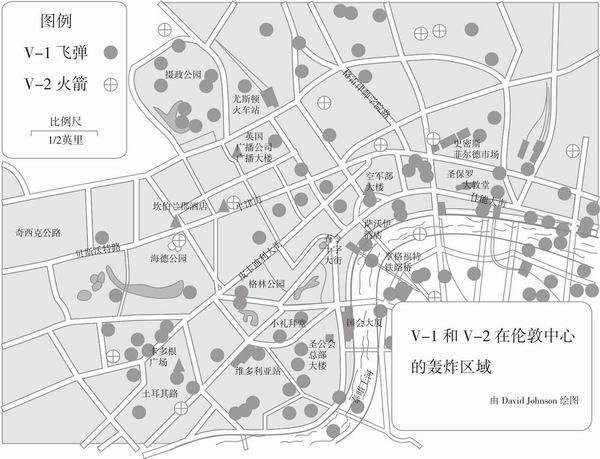
图7.1　伦敦V-1和V-2炸弹命中模式

从地理图式中推断因果关系的倾向还有一个很现实的例子，是有关“癌症集群”癔症的心理学。在过去的20年中，有关某些社区中癌症发病率奇高的报道越来越多（见Gawande，1999）。当一个社区注意到当地的癌症发病数量不同寻常时，自然而然就会想要在环境中寻找原因——水、陆地或空气中的某些东西，但如果对被隔离的癌症高发地进行调查，却往往一无所获。面对局部地区不断上升的癌症率，一些公共卫生机构每年开展了数以千计的“热点追踪”研究。但（在1999年）加利福尼亚首席环境健康调查员雷蒙德·理查德·尼特拉指出，在成百上千的此类公开调查报告中，没有一个明确地指出了某种环境因素（引自 Gawande，1999）。在这些调查中，只有一个调查发现了一个不明致癌物质。尼特拉指出，在美国公共卫生署有80种不同的典型癌症登记在册，根据概率论的预测，在加州5 000个普查统计报告中，你能够在其中2 750个报告中观察到某种癌症的发病率在统计上显著过高，但这种情况只是随机的结果。因此，如果检查一下你的邻居们在那80种癌症上的发病率，那么有0.50以上的可能性他们会至少在某1种癌症上的发病率显著过高——但是这样的发现与一个假定没有任何环境因素参与的随机影响模型是完全一致的。艾伦·本德（引自Gawande，1999）是明尼苏达州卫生部门的一名流行病学家，他对这些由社区癌症集群所引发的热点追踪调查作如是评论：“实际上这完全是在浪费纳税人的钱。”

但是我们应该做些什么来维持公众信任，并发现真正的环境卫生风险呢？事实上，一个随机概率模型与我们观察到的模式相一致，并不能证明其中不存在因果关系——这又回到了那个问题：“你怎么能证明这个效应完全不曾存在于任何地方？”但是我们会将这些事件的重要性情感化和符号化，浪费大量的公共资源去应对，并且错误地发现了集群与其周围环境之间的许多相关。对个人集群进行分析，并且寻找这些集群与某些（任意）环境因素之间的关联，这样的策略被流行病学家们称为德州神枪手谬误（Texas sharpshooter fallacy）。这个说法源自一个火枪手的故事，这个火枪手朝着一个谷仓的墙壁射了一串子弹，然后在这些弹孔周围画上一圈圈的靶心。在这种情况下，我们需要接受那些统计专家们的意见，只有在之前已经有充分的理由假设出一种环境因素，或者确实存在极为不同寻常的统计模式时，才对之做出反应。一个广受关注的癌症集群案例发生在马萨诸塞州的沃本恩，在同名为《法网边缘》的图书和电影中均有详细描述。这个案例最终也没有发现由瑞利皮革厂排放的污染物与工厂周围居民的癌症病例之间存在科学可靠的因果关系。

7.4 趋均数回归

对含有随机（未知因素）成分的事件进行代表性思维还会带来一个问题，就是会使我们做出一些非回归预测。要了解为什么会出现这样的情况，我们首先要了解什么是回归预测。

假设一些父亲的身高都非常高，那么平均来说，他们的儿子也会是高个子，但是会比他们的父亲要稍微矮一点。同样，特别高个儿子的爸爸平均也会比他们的儿子矮些。我们看图7.2中，首先，横轴表示父亲身高，纵轴表示儿子身高，椭圆表示“数据”，我们以那条垂直实线代表高个父亲，这条线与椭圆形成上下两个交点，而因为儿子的身高在垂直维度上的分布可能并不是绝对对称的，会朝矮个儿子的方向有一个长尾，因此，高个父亲的儿子平均身高就可能在水平虚线的位置，即那条标有“高个父亲的儿子身高均值”的虚线。这样通过考察一个典型的“高个父亲”，我们就能由一个简单的逻辑来确定这些父亲的儿子的平均身高，结果显示这个均数出现了“回归”——也就是说，儿子的身高相比这些父亲的极端身高，变得不那么极端了。d与D’之间的差异就是这个数据集的回归程度指标。如果我们从“高个儿子”入手，会发现一个完全一样的反转模式，水平实线表示“高个儿子”，由垂直虚线向交于轴（x轴）的那一点，即为高个儿子的父亲的平均身高。

英国科学家高尔顿（1886）第一个发现了这一关系，他将其命名为“后代趋中回归”（filial regression towards mediocrity）（p.246）。一开始，他认为这种关系来源于某种遗传过程，这种遗传过程使有机体朝着平均属性转变，但是在考虑了逆转关系（时间上倒转）后，他得出结论，认为这是所有相关关系中都存在的统计属性。图7.2解释了这种关系，你看到的就是一个简单的趋均数效应。因为父亲和儿子的身高并不完全相关（无论出于什么原因），所以就存在回归。非回归预测（non-regressive prediction）是指人们存在这样一种倾向，即忽略一些隐蔽的回归关系，而预测极端值会与一些异常极端值相联系——就如我们马上会看到的那样。

我们来考虑另外一个例子[来自Quinn McNemar（1940）的工作，Quinn McNemar是一位心理学家，也是最早指出这个统计结果并说明其对人类行为研究的启示的学者之一]：假设在一家孤儿院中对所有的孩子进行一项智力测验，施测两次，期间相隔一年。再假设两次测验的群体均数和标准差都相同，但是两次测验分数之间并不完全相关（实际相关大约在+0.80）。现在只考虑那些在第一次测验中得到高分的孩子：他们第二次的测验分数平均来看会低一些。（因为相关系数低于+1.00，我们预期其中会有一些变化；因为两次分数的分布是相同的，因此第一次测验中的高分者平均说来一定会在第二次测验中稍低一些。）那些最低分的孩子同样如此：第一次测验的低分孩子在第二次测验中平均分数会高一些。如果我们将时间逆转，从第二次测验看到第一次测验，结果又会怎样呢？答案是同样的，这种关系也能够成立——极端分数会变得不那么极端。趋均数回归对于不完全相关的量化变量来说是必然的。

图7.2　统计回归解释

也许最容易理解回归的方式是考虑完全回归的极端情况。抛8次硬币，随后重新再抛8次。无论第一个序列中有几次正面，第二次序列中正面次数的期望（平均）都为4，因为硬币是没有动过手脚的，所以第一个序列中的正面次数与第二个序列中的次数是完全不相关的——因此就是取平均，也就是4，这是完全的趋均数回归。随着变量之间的预测力提高，回归程度就会降低。举例来说，平均而言，非常高的父亲所生的儿子都高于普通人，但是不如他们的父亲高。只有当一个变量完全能由另一个变量预测的时候，才不存在回归。事实上，标准相关系数（的平方）可以很简单地定义为一个变量由另一个变量进行线性预测的非回归程度。趋均数回归的技术定义为完全相关（即+/-1.00）与线性相关之间的差异：

回归 = 完全相关-相关

在日常判断中，有许多例子证明我们会忽略趋均数回归。我们常常会惊讶于为什么在一次华尔街的突出业绩、一部热门电影、一支榜首歌曲或一次比赛优胜之后人们就表现平平了。《体育画报》封面厄运就是一个经典的例子。读者们发现，每当一个运动员或一支球队上了《体育画报》的封面（这常常是因为他们取得了一些优异的成绩）之后，这个人或这支球队就可能会表现低迷，或者遇到其他一些不幸。统计分析更是强化了这种印象，而球迷们则为这样的现象提出了许多看似合理的解释——这个运动员因为出名而骄傲、因为媒体的追逐而分心，等等。当然，我们知道大部分（即便不是全部）的“效应”其实是因为人们选择了极端事例并观察到了趋均数回归，“选择性极端事例”这样的解释就已足够，不需要再加入其他特别的解释了。

霍雷斯·赛克雷斯特在1933年的《商业中庸才的胜利》一书中举了一个学术方面的经典例子。赛克雷斯特的观点是，成功和不成功的企业“都会走向平庸”，这个观点通过上百幅企业业绩图得到证明。这些图显示，在第一年选出的业绩处于两极的公司中，最为成功的那部分企业之后会变得不那么成功，而最初最不成功的那些企业则会慢慢向成功的方向发展。杰出的统计学家Howard Hotelling对此评论道：“这种表面上的汇聚情况是一种由分组方法导致的统计谬误，这些图表最多只能证明各组企业的比例会产生波动。”他指出，要验证数据是否真的出现趋向于中间的汇聚，应该考察各组企业之间的方差是否随时间持续降低——但在这个研究中并没有考察。同样的错误也出现在彼得斯和沃特曼在1984年的畅销书《追求卓越》一书中。这两位管理咨询师挑选了43家业绩优异的公司，评述了一些能够使这些企业走向“卓越”的突出特点，但5年之后，《商业周刊》的封面故事《哎呀，现在谁还是卓越的？》指出，在最初那些因为卓越而入选的公司中，超过三分之一正面临财务危机或破产。

在许多案例中，我们都非常关心各种改善绩效的方法所产生的效果——对成绩不良的学生进行课程辅导、奖励业绩突出员工、为身体欠佳者补充营养等。在这里，我们再次遇到这个问题，需要将这些方法实际产生的效果和单纯的回归作用区分开来。这个问题只存在于极端事例中，有些随之而来的错误是非常隐蔽的。比如在二十世纪六十年代中期，当Daniel Kahneman（Tversky & Kahneman，1974）向以色列国防军的飞行教官们解释奖励比惩罚具有更好的激励作用时，一个教官向Kahneman提出了反对意见。

尊敬的先生，您所说的只对实验室里的小鸟有用。我常常热烈地表扬出色完成飞行练习的士兵们，但是下一次他们几乎都会做得比前一次差；而当士兵们表现得很差时，我会对他们发火，于是下一次他们的表现基本上都会进步。别告诉我奖励有用而惩罚没用，我的经验正好相反。

这位飞行教官看到的就是一个回归效应。人们在“出色完成飞行练习”后会倾向于做得没那么好，这是因为一次表现与下一次表现之间并不是完全相关（同样，无论出于什么原因）。每次“表现得很差”之后同样会有所进步——同样只是因为每次表现之间并不是完全相关的。（要在某个学期获得“学业进步”奖，最简单的方法就是前一个学期的成绩在班级里接近垫底，而得到“后进生”称号的方法就是在某次能力测验上得个高分。）遗憾的是，就像飞行教官的故事一样，许多不了解回归效应的教师也许就会系统性地认可惩罚的作用（因为极端的不佳表现会朝着较好的方向回归）而对奖励失望（因为极端的出色表现会朝着较差的方向回归）。（事实上，要说明为什么一些像飞行教官这样的人会偏好用惩罚而非奖励作为一种行为操控的手段，回归效应的解释就足够了。）

我们对这些不可避免的回归效应视而不见，这还会带来一个令人不快的副作用，那就是，我们对于一些通过解雇教练或CEO来获得成功的干预方式存在过度自信。考虑这样一种典型的情境：在某个赛季的上半赛季，某支球队表现得特别糟糕，球队老板于是决定解雇教练，在随后的下半赛季，球队的表现转好了。我们应该将这种改善归因于解雇并替换教练，还是归因于简单的回归效应呢？毕竟总体来说，赛季中段解雇教练这样的事情往往是在球队表现极为糟糕的情况下发生的。因为我们缺少这样一个随机解雇教练的实验（而且这样的实验不太可能实现），所以无法确定到底是哪种因素在起作用。但是谨慎的统计分析一致显示，大部分的进步都是因为回归作用（Koning，2003），解雇公司经理人的情况同样如此。（体育运动中的实际情况是这样的：如果一个球队在某个赛季的上半段表现非常差，通常很可能是因为他们遇到的对手都是一些强队，而后半赛季往往就会遇到一些弱旅，从而更大程度地夸大了替换教练所带来的作用。）

应对回归效应的理性方式是，在做出预测的时候把“回归”考虑进来。因此，当我们需要或想要评估差异（比如，应该奖励“优秀表现”还是改善“糟糕表现”）的时候，要比较实际值和预测值（predicted value）——不要用两次测量中的实际值来进行比较。举例来说，当我们要比较一个病人在时间点1和时间点2上的MMPI测试得分，以此考察这个病人的“进步”时，首先用相关的方法由各个得分得到每个病人在时间点2的一个（回归的）预测分数，然后将时间2的实际得分与这个预测分进行比较，而不是比较时间2和时间1的实际得分。否则的话，那些在时间1上（病理）得分较高的病人们可能会被误判为“进步”了（“他们的分数已经无法再高，只能往下走”），而那些MMPI得分正常的病人可能会被误判为治疗不起作用。遗憾的是，代表性思维就会使人们在不做回归的情况下直接比较差异，这显然会导致错误的结果。举例而言，“最值得注意的是，那些在症状改善方面得分最高的人……正是那些最初症状最为严重的、最没有希望用保守疗法的人”（Dawes，1986）。（道斯在其作为一名临床心理实习医生时，他请医院的心理学家和精神病学家将一些出院的病人划分为进步程度高于平均和低于平均两组，结果那些归类为进步程度高于平均的病人，都是住院期间在各种MMPI测试中得分较高的人——相对于大部分接受治疗的病人来说，其得分差异显著。）

我们试图评估一些用来提高绩效的干预手段（比如飞行教官试图用惩罚糟糕表现的方式来提高学员表现）是否成功时，趋均数回归就特别容易蒙蔽我们的判断。如果采用干预手段是因为“我们出现了问题”，就意味着我们很难清楚地了解干预手段的效果。比如，在发生惨绝人寰的交通事故之后采用一个严格的交通管理计划、在公司几次糟糕的业务表现之后聘请一个新的CEO、在连输几场比赛后换一个新的教练，这些情况下我们都不可能准确地评估其中的因果关系。干预手段能否起到改善的作用，这一点存在偶然性，而几乎可以确定的是，其中一部分或绝大部分的效应来自于趋均数回归。

7.5 关于我们无法接受随机性的反思

前面所描述的判断中的一些错误，对我们来说可能已经不是那么出人意料了。赌场经营者们花了几百年的时间来美化坑人的概率游戏的形象，就是为了引诱那些不够警惕的顾客，我们怎么能精明过他们呢？同样，在哪些条件下（在某些体育项目中）确实会出现连胜的情况、而在哪些类似的情况下则不会出现，球迷们又怎么会分得清楚呢？我们就是会看到很多实际不存在的因果结构，面对许许多多自然发生的情景时会想象自己在其中有更多的控制能力，为什么会存在这种普遍倾向？这依然是一个让人疑惑的问题。在下一章中，我们会介绍一个良方来应对这些难以根除的坏习惯——像一个概率理论家那样思考。

参考文献

Bayer, D., & Diaconis, P.(1992).Trailing the dovetail shuffle to its lair.Annals of Applied Probability, 2, 294-313.

Bilefsky, D.(2008, April 26).Serbia’s most famous survivor fears that recent history will repeat itself.New York Times.Retrieved June 20, 2009, from https://www.nytimes.com/2008/04/26/world/europe/26vulovic.html

Dawes, R.M.(1986).Representative thinking in clinical judgment.Clinical Psychology Review, 6, 425-441.

Diaconis, P., Holmes, S., & Montgomery, R.(2007).Dynamical bias in the coin toss.Society for Industrial and Applied Mathematics Review, 49, 211-235.

Feller, W.(1968).Introduction to probability theory and its applications (3rd ed.).New York: Wiley.

Fenton-O’Creevy, M., Nicholson, N., Sloane, E., & Willman, P.(2003).Trading on illusions: Unrealistic perceptions of control and trading performance.Journal of Occupational and Organizational Psychology, 76, 53-68.

Galton, F.(1886).Regression towards mediocrity in hereditary stature.Journal of the Anthropological Institute of Great Britain and Ireland, 15, 246-263.

Gawande, A.(1999, February 8).The cancer-cluster myth.New Yorker, pp.34-37.

Gigerenzer, G.(2006).Out of the frying pan into the ire: Behavioral reactions to terrorist attacks.Risk Analysis, 26, 347-351.

Gilovich, T., Vallone, R., & Tversky, A.(1985).The hot hand in basketball: On the misperception of random sequences.Cognitive Psychology, 17, 295-314.

Hotelling, H.(1933).Review of The Triumph of Mediocrity in Business.Journal of the American Statistical Association, 28, 463-465.

Kareev, Y.(1992).Not that bad after all: Generation of random sequences.Journal of Experimental Psychology: Perception and Performance, 18, 1189-1194.

Koehler, J.J., & Conley, C.A.(2003).The “hot hand” myth in professional basketball.Journal of Sport & Exercise Psychology, 25, 253-259.

Koning, R.(2003).An econometric evaluation of the effect of iring a coach on team performance.Applied Economics, 35, 555-564.

Langer, E.J.(1975).The illusion of control.Journal of Personality and Social Psychology, 32, 311-328.

Langer, E.J., & Roth, J.(1975).Heads I win, tails is chance: The illusion of control is a function of the sequence of outcomes in a purely chance task.Journal of Personality and Social Psychology, 32, 951-955.

Larkey, P.D., Smith, R.A., & Kadane, J.B.(1989).It’s okay to believe in the “hot hand.”Chance, 2(4), 22-30.

Lopes, L.L.(1982).Doing the impossible: A note on induction and the experience of randomness.Journal of Experimental Psychology: Learning, Memory, and Cognition, 8, 626-636.

McNamar, Q.(1940).A critical examination of the University of Iowa studies of environmental inluences on IQ.Psychological Bulletin, 18, 63-92.

Meisler, S.(1977, December 30).Spain lottery-Not even war stops it.Los Angeles Times, p.D1.

Oops! Who’s excellent now？ (1984, November 5).BusinessWeek, 76-88.

Peters, T.,&Waterman, R., Jr.(1984).In search of excellence.NewYork: Harper & Row.

Poincare, H.(1952).Science and method (F.Maitland, Trans.).London: Dover.(Original work published 1914)

Sagan, C.(1997).The demon-haunted world: Science as a candle in the dark.New York: Ballantine.

Secrist, H.(1933).The triumph of mediocrity in business.Chicago: Bureau of Business Research, Northwestern University.

Sivak, M., & Flannagan, M.J.(2003).Flying and driving after the September 11 attacks.American Scientist, 91, 6-8.

Tversky, A., & Gilovich, T.(1989).The -hot hand-: Statistical reality or cognitive illusion.Chance, 2(4), 31-34.

Tversky, A., & Kahneman, D.(1974).Judgment under uncertainty: Heuristics and biases.Science, 185, 1124-1131.