第8章 理性思考“不确定性”

8.1 面对偏差，我们该怎么办

尤利塞斯在听到塞壬的歌声之前就聪明地把自己绑在了桅杆上[1]。他这样做并不是因为害怕塞壬，而是因为害怕自己对塞壬歌声做出的反应。于是，他事先做好了防范措施。同样，自动化思维造成的认知偏差就像海妖的歌声，以一种可预知的方向，将我们的判断引入歧途。我们必须采取预防措施，避开这些未经审视的判断所设下的圈套。

本书的目的之一就是教会读者对判断过程进行分析性思考。我们认为，要系统地分析一个判断，最好的方法就是学习一些概率论和统计学基础知识，并将之应用于重要的判断过程。拉普拉斯[2]有一句著名格言：“概率论本质上只是一些计算方面的常识（p.196）。”其实，任何学过或者教过概率论的人都会知道这句话肯定是错误的，因为概率论的发明只不过是近期的事情，而且我们的头脑似乎天生就不是按这些概念来思考的，何谈“常识”？本书的前七章可以理解为是对违背（有时甚至是根本抵触）概率论的认知习惯所做的总结。本书附录中提供了一些基本概率论基础的总结，而在本章中，我们将辅之以具体事例来阐述概率思想的本质。

曾有人尝试训练人们不要根据代表性来思考，或者不要受可用性或其他偏差的影响，但是多数情况下都不太成功。我们在思考过程中在事物之间建立简单联系的情况实在是太普遍了，以至于早期英国的实证主义者认为这种“联系”是我们思维的基础单元。再者，基于经验来做判断是十分合理的，而且对我们的生存至关重要。

所以，我们需要另一种方法，能在必要的时候，至少是在我们做重要判断时，将我们从依赖直觉、联系、启发式的歧途上引导回来。预防偏差的其中一个选择是利用外部帮助。例如，一个临床心理学家能够在纸上、在电脑里记录案例（例如，自杀威胁），然后利用符号公式或图表来编码数据以估计案例发生的频率。把度过的每一周用一个简单的图表来区分“好”或“坏”就可以揭示出或者否定一个模式。又或者仅仅记下基础概率、尝试去应用基本的概率论，也能够避免很多不理性的判断。

我们在本章中将要举例说明如何利用外部帮助，而利用这些外部帮助的最大阻碍是说服我们像尤利塞斯那样对自己采取预防措施。自我施加的外部约束实际上更能增加我们的自由度，因为它能使我们从一些可以预见的、讨厌的内部限制中解脱出来——这个道理虽简单，但不太为人们所意识。并非人人都能成为尤利塞斯。而这些内部限制既可以是情感层面的也可以是认知层面的，这一观点更难以得到认同。因此很多人认为，让自己的判断建立在“纯数字”或图像或计算机结果的外部帮助上是一件令人极其厌恶的事情。事实上，甚至有证据表明，当存在外部帮助时，不少专家试图在这些外部帮助的预测之上再根据自己的直觉去改进他们的判断，但结果呢？反而比不动脑地相信外部预测更糟糕。可能性的估算的确只涉及纯粹的数字，但正如Paul Meehl（1986）所指出的那样：“当你从超市出来的时候，你不会打量一下你买的那堆商品然后问服务员：‘我觉得这些东西大概是17美元，你觉得呢？’，你当然不会这样的，你会进行计算。”（p.372）计算、跟踪记录和明确写下概率论推断的规则，能够极大地帮助我们战胜由代表性思考、可用性思考、锚定-调整以及其他偏差引起的系统性错误。如果能做到这些，我们甚至能够从经验中学到一些东西。

8.2 开始用概率来思考

现代概率论起源于富有的贵族们雇用数学家来帮助他们赢得与熟人之间的博弈游戏（就像第1章Cardano的例子一样，只不过他是给自己建议）。概率分析最基本的规则应该是，告诫人们在分析过程中要从全局视角审视情境（任何情境，包括掷骰子游戏、博得市的交通问题、匹兹堡的犯罪问题甚至是膝盖疼痛的情况），然后定义一个包括所有可能事件的样本空间，并确定这些事件间的逻辑关系。以上步骤就是理性分析与那些以可用性、相似性、情景建构为基础的判断的分歧所在：当我们根据直觉进行判断时，思维会被拖入一个有限的、有系统偏差的可能事件的子集。例如在情景建构中，我们经常陷入情景的细节，只注意到一个特定的（而且是荒谬的）结果路径。

Daniel Kahneman和Dan Lovallo（1993）指出，决策者倾向于强调每个问题的独特性，并做“内部观察”（inside view）。他们提出的补救办法跟本书一样，就是慎重地进行外部观察（outside view），也就是说，把当前问题看做一系列类似问题中的一个，并将概率思想应用其中。为了阐明外部观察的重要性，Kahneman讲了一个他亲历的设计某个新课程的故事：

那个团队运作了一年，并取得了一些重要的成果，在某次团队会议上我们的讨论转到了这个项目还会持续多长时间这个问题。为了使讨论更加有效率，我请每个人在纸上写下他们估计再要多少个月才能向教育部提交一份完稿。结果，大家（包括我自己在内）估计的时间是18~30个月。此时，我突然产生了一个想法，询问团队中的一个成员（他是课程设计的著名专家）：“我们肯定不是惟一一个设计新课程体系的团队。你能不能回忆一下以往类似的例子，想象其他团队也处于与我们现在类似的阶段，你觉得他们还需要多久才能完成项目呢？”一段长时间的沉默过后，他用明显带着不安的声音说道：“首先，我得说并非所有处于与我们类似阶段的团队都完成了项目，大概40%的团队最终放弃了。至于剩下的，我想不起来有任何一个团队是在7年之内完成项目的，当然也没有多于10年的。”他进一步补充：“我想不出我们优于其他团队的地方。不得不承认，根据我的印象，我们的资源和潜力似乎还稍有点低于那些团队的平均实力。”（Kahneman & Lovallo，1993，p.24）

我想通过这个故事说明的是，如果判断时能够退一步做外部观察，并从整体分布和概率的角度来思考，即便这一思考只是定性的，也能使判断更为准确。如果能基于系统收集的数据和概率论中的定量规律来思考的话，判断就会更好。

概率论用精确的术语来描述基本事件、事件集及它们之间的关系。让我们从一个定义明确的例子开始：掷两枚骰子。首先，骰子朝上那一面的数字可称为一个最简单的事件，比如“我掷出一个1”；第二，两个简单事件的合取，比如“我两颗骰子分别掷出1和6”，（顺序任意）；第三，两个简单事件的析取，比如“我掷出一个1或一个6，或1和6同时出现”（有时这叫做“或”逻辑）。第四，条件事件，就是某事件的发生以另一个事件的发生为前提，比如“当我掷出的两个骰子点数合计为7时，其中一个为1”。如果两个骰子是均匀正常的，我们就可以系统地描述共包括36种等概率事件的样本空间——你掷一个骰子的结果可能是1到6中的任何一个数字，另一个骰子所得结果也是如此，这样就共有6 × 6种可能的合取事件。

在明确了可能事件的样本空间后，我们希望知道简单事件和相关事件在样本空间中的频率和概率。在理想化情境中，我们可以按逻辑推导出骰子、扑克牌和其他可靠的赌博设备中的事件类别、频率和概率。比如，因为骰子的六个面中有一面是1，因而我们说1出现的概率是1/6；在36种情况中，同时掷出1和6共有2种情况，于是我们有2/36的概率掷出这一合取事件；此外，我们有20种情况掷出一个1或一个6，或者1和6，于是我们有20/36的概率掷出这一析取事件。最后，对于条件事件“给定两个骰子和为7，而其中一个是1”，我们把条件限制在“和为7”，则可以计算出“其中一个是1”的概率是2/6，因为共有6个事件满足和为7，而在其中2个事件里有一个骰子被掷出了1。现在我们考虑定义不那么精确的情形：假设我们想研究大学生的一些特征。如果我们随机从芝加哥大学的学生中选出一个，那么选到女生的概率是多少？2008年芝加哥大学有5026名学生，其中2513名是女生；因而随机选到女生的概率是2513/5026，接近0.50。那么选到物理专业学生的概率呢？有815名同学选择物理学作为自己的专业，所以随机选择到物理专业学生的概率是815/5026，约为0.16。那么，选到一个物理专业的女生的概率呢（这是一个合取事件）？ 共有211名同学既是女生又学物理，因而概率是211/5026，约为0.04。若考虑到析取事件，物理专业学生或女生这两个条件至少满足一个的共有3117人，其概率为3117/5026，约为0.62。而物理专业中女生的概率呢（这是一个条件事件）？我们只需考虑学物理的815名学生，然后求从他们中选到女生的概率即可——其概率为211/815，约为0.26。这是另一个能准确定义区分事件的例子（我们假设女性、物理专业都能被准确定义），因此我们能够通过经验频率来推断概率（而不是像骰子那样通过理想的、逻辑的频率来推断）。需要注意的是，反向的条件概率——即给定女生这个条件而选到学物理的学生的概率（211/2513或0.08）——与之前所说的给定物理专业为条件而选到女生的概率（211/815或0.26）并不一样。一般而言，一个条件概率并不等于其相反的条件概率，正如第5章所阐述的比例规则那样，例如，p（女生物理专业）≠

p（物理专业女生）。再考虑一个更加模糊的情形，在这种情形中我们只能确定事件的集合和范围，却无法统计频率。假设我们正在考虑共和党是否能赢得2012年美国总统大选。当我们在2008年写这本书的时候，民主党的候选人是奥巴马（现任总统），但对4年后的共和党候选人却所知甚少。一些成功州长的名字一直在流传，如Sarah Palin（阿拉斯加州），David Petraeus将军（当今最有名的军事领袖），和Newt Gingrich（前众议员，现为保守派权威），但没有人知道谁将在4年后被提名为候选人，甚至奥巴马的候选人资格也仍不确定，因为他的第一个四年任期必将充满了各种变数。然而，概率分布依然是帮助我们分析情境和作出预测的最好方法。我们可以列出大部分可能出现的事件，比如两党下一届候选人的提名、对两党和全民公投可能产生影响的不确定事件（如经济条件、个人丑闻、医疗问题、领袖因素、竞选资金等等）。在这种情况下，系统地列出这些事件并不能使我们对这些事件发生的确切概率有把握，但却能够提醒我们未来有多么不确定，提醒我们别目光短浅，别仅仅着眼于某一种可能情况并对其抱以过多信心。尽管有些模糊，但分布表征和概率分析相对于直觉判断已是一个重大进步。然而，我们不太可能主要依靠鲜活的、独立的事件的相对频率作判断——尽管当我们失误时会去参考可能有关的统计资料，如p（现任总统获胜的概率）。但是，当我们基于情境和某个结果的可能原因来推理时，审慎地尝试去系统表征这些问题也能够提高我们判断的连贯性和准确性。

让我们考虑一个更严重的情况：在未来十年中会出现一国针对另一国的核武器部署吗？在这里连情境的结果都无法明确定义：如果恐怖组织（也许不能归于任一国家）引爆了某个中东国家的核设施，这算是核武器部署吗？我们设想的情景（对具体的可能结果的描述）是模糊的：“联合国维和部队与非洲某组织间的小冲突逐步升级……”，“一个针对以色列领导人的刺杀失败了，那么其报复行动……”在这里，似乎没有相关频率可以计算。未来的情形将不同于我们所能想到的任何历史上的情形。但我们仍然相信系统分布方法是做概率估计的最好方法，虽然存在不确定性，但是有可靠的依据。事实上，Asher Koriat、Sarah Lichtenstein和Baruch Fischhoff（1980）的心理学研究表明，仅仅列出一些相关事件并系统地考虑每个事件发生和不发生的原因，就能提高我们的判断质量。

通过这些例子我们想表明什么呢？第一，我们介绍了可以根据集合内成员间的基本关系对事件进行概率描述。第二，我们介绍了四种可能需要概率描述的情境：（1）传统的机会游戏情境（比如掷骰子），在这种情境中，理想的随机设备为潜在的问题提供了良好的描述，因而逻辑分析能够用于推断概率；（2）定义明确的“实证”情境，在这种情境中，相关频率的统计信息能够用来计算概率（例如，我们对于芝加哥大学学生类别的判断）。（3）中等定义明确的情境，我们必须根据因果关系和偏好而不是相关频率来推理（比如预测下届美国总统大选的结果），但在这种情境中，稍加思考就能够定义非常完整的相关事件及其样本空间；（4）大量未知情况的情境，在这种情境中，即便是相关事件的样本空间都难以建构，而且似乎也不存在相关频率（例如，未来十年的国际冲突）。

概率论的一个显著特征就是，四大公理（见附录）提供的法则可用来进行理性推理，尽管对于这些数字究竟代表什么仍有大量的争论。以上选出的四个例子是为了给读者一个关于用概率进行解释的整体感觉：它是基本演绎逻辑的扩展；是基于外部事件发生频率计算出的实际数字；是对头脑中的主观可信度而非外部世界的量度。

第三，对不确定事件进行判断与推理时很多错误都源于这个过程的最初阶段，即人们对需要判断的情境进行理解的时候。如果人们能够对将要判断的情境建立真实表征，并在整个推理过程中不断理清集合中成员间的关系，那么就能避免很多错误。当然，关于概率和随机过程也有很多误解，但很多时候，在还没有来得及综合分析不确定性信息之前，我们的判断就已经出现了偏差。如何在不确定的情况下做出更好的判断，我们的主要建议是，对于将要判断的问题和情形，建立一个有效的外部表征（图示的和符号的）。

8.3 理解判断的情境

尽管从直接经验中建立一个情境模型可能会更加困难，但仅仅基于一段对新奇而不确定情境的书面描写来建立一个可理解的情境表征也不容易。Raymond Nickerson（1996）在一篇关于概率问题的语义模糊性的论文中列举了理解阶段可能犯的多种错误。其中，一些流传已久的例子在脑筋急转弯这类畅销书籍中被奉为经典。让我们从一个在概率推理领域经多次研究过的简单问题开始（作者为Maya Bar-Hillelt和Ruma Falk，1982，p.119）；试试下面这个游戏，在继续阅读后面的文字之前做出自己的估计：

帽子里有三张卡片。一张两面都是红色（“红-红”），一张两面都是白色（“白-白”），一张一面红色一面白色（“红-白”）。从里面随机抓出一张卡片扔向空中，落地后红色一面朝上。问：这张卡片是“红-红”的概率是多少？

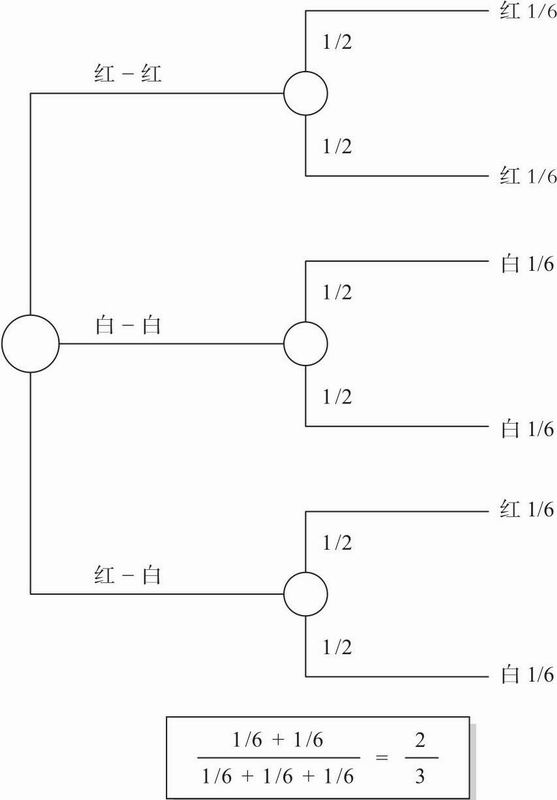
图8.1　表征三张卡片问题的概率树

通常的回答是“1/2”或“0.50”（在Bar-Hillel的实验中，有66%到79%的参与者给出这个答案）。对这些参与者的访谈表明，对于这个问题他们有一个典型的判断模式：“因为这张卡片红色向上，我们知道它不是‘白-白’卡，而由于还剩下两种卡片，于是它有50%的概率是‘红-红’卡。”这表明，纸上的文字叙述导致被试形成了“先有三张，剩下两张”的问题表征。然而，正确的问题表征是根据卡片的面，而不是整张卡（见图8.1；Brase，Cosmides，& Tooby，1998也指出了这点）。所有结果的样本空间包括六个事件——每张卡片的每一面各为一个事件。由于红色的一面向上，因此在“有效样本空间”中共有三个事件：红白（红面向上）、红-红（一个红面向上）、红-红（另一个红面向上）。因此正确答案是2/3——三个等概率事件中，其中两个是红-红。

某流行杂志中的“向玛丽莲提问”专栏发表了一个更为复杂的问题，这个问题受到了相当多的关注，因为其答案出乎大多数人的意料，并且足够深奥，以至于引起了很多著名数学家的争论（vos Savant，1991；Deborah Bennett在她介绍概率论的著作Randomness[1998]中提供了对这个问题的总结）：

假设在一个游戏节目中，有三扇门供你选择。其中一扇门后面是一辆豪华轿车，而另两扇门后面都是山羊。你选择了一扇门（比如1号门），之后，知道每扇门后面分别有什么的主持人打开了另一扇门（比如3号门），门后是只山羊。这时主持人对你说：“你想选择2号门吗？”，即改变主意选择2号门是明智的吗？（vos Savant，1991，p.12）

这个脑筋急转弯问题的第一个难点是各种“可能事件”所包含的惊人的复杂性。试一试用图表来系统地列出每一个相关事件：参与者可以选择三扇门，轿车藏在哪里共有三种可能（这样一共有九种情境）；主持人可以打开不同的门（主持人究竟面临几种选择会因碰到九种情境中的哪一种而有所不同）。之后，参与者的两种选择（改主意或不改主意）使这个问题更为复杂：共有18到36种情况——这取决于解决问题者对问题采用的不同表征。

这个脑筋急转弯问题的另一个更加困难的地方在于，对主持人选择打开哪一扇门的规则描述得很模糊；除非这种模糊性被解决了，否则难以用唯一的样本空间对这个问题进行表征。根据问题的描述，主持人的规则至少有三种可能的解释。第一种规则，主持人总是随机打开没有被参与者选择的门（例如，在上面的情境中，主持人掷一枚硬币来决定打开2号或3号门）。这表示主持人可能打开一扇门并展示出门后的轿车，然后（和观众一起）笑话你选错了门，游戏结束。但也存在第二种规则：假设主持人总是挑选后面藏着山羊的门打开，决不打开参与者挑选的门；当参与者已然选中了藏有轿车的门，主持人就随机打开一扇门。这样，参与者的选择和主持人开门之间的关系就更复杂了。但是还存在更加复杂的第三种规则：假设主持人总是挑选藏有山羊的门打开，决不打开参与者挑选的门；在参与者已然选中了藏有轿车的门之后，主持人有偏向地挑选剩下两扇门中序号较小的一扇打开（针对这种规则可能存在其他偏差）。尽管这三种规则均符合上述问题的表述，但其潜在概率却各不相同。

对这个问题最普遍的表征是，主持人总是打开与参与者最初选择不同的门，且绝不会打开藏有轿车的门（即遵循上文第二种规则）；于是，参与者改变主意就可能提高但绝不会降低得到轿车的概率。因此，基于这种表征，问题的答案是参与者应该改变主意。在图8.2中，我们提供了清晰表征这个问题的概率树。这里要说明的是，问题表征是概率推理过程中最基本的、起决定性作用的第一步。这个“三门问题”的模糊表述引发了很多困惑和争议，很多学术期刊的讨论也随之而来，可是要想把这个问题毫不含糊地表述清楚，本身也是件极其复杂的事情。而实际上，现实世界的不确定性和决策的模糊性比这个问题要更加令人生畏。

学习概率和统计课程的主要好处在于，我们有机会练习将情境转化为更精确完整的表征；或者在复杂的真实世界中，练习提取最基本的不确定事件和因果联系。我们介绍了表格、概率（或决策）树以及韦恩图，用以描述本书中大多数判断和决策情境。然而，这些合适而有效的图表是应待解决的特定问题的不同情况而创造的。我们会首先尝试树状图，因为总的来说它们最有效，但有时其他图表会更有启发意义。幸运的是，构建这些表征的技巧是任何一位愿意学习的读者都能通过练习掌握的，第一步就是学习本书中的例子。

进一步讲，思考概率问题时，用频率来表示某个事件在相关子集中出现的情形，通常更有利于形成准确的判断。当人们想象个体、客体或事件的频率时，就可以更好地分析总体中某些部分之间的联系。事实上，当鼓励人们学会基于频率而非可能性去表征情境时，前几章中所阐述的许多判断错误都会大大减少（例如Gigerenzer & Hoffrage，1995；Sedlmeier & Betsch，2002）。频率图表对于减少人们关于条件概率[例如，p（癌症阳性检验结果）对p（阳性检验结果癌症）]和合取谬误（类似“琳达更可能是一位女出纳员而非出纳员”的描述）的迷惑是非常有用的。

下面，我们将回顾不确定性条件下理性判断的概念，然后再回到我们的主题，即如何清楚地用分布的形式来表征需要判断的情境。

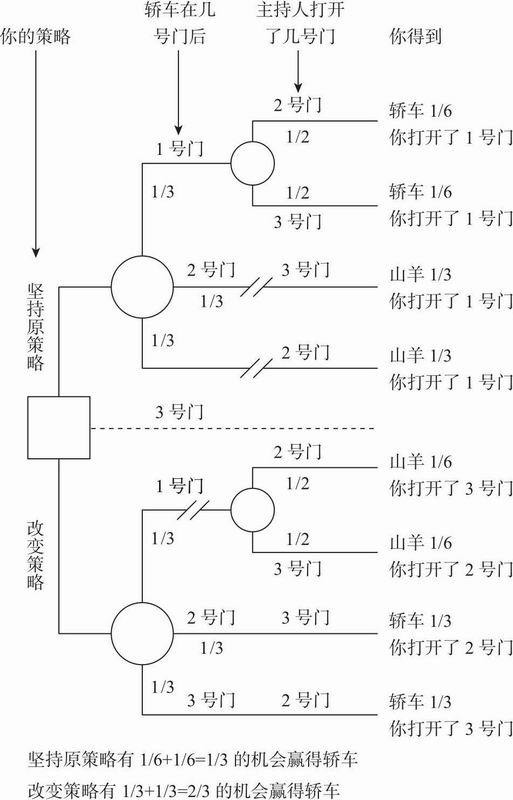
图8.2　最初选择1号门之后用概率树来表征三门问题（这只表征了三分之一的可能性——当你先打开2号或3号门时，可以画出两个相似的概率树，这样就穷尽了所有可能性。）

8.4 理性的测试

在本书的前半部分，我们提供了许多不准确或非理性判断的例子。我们基于什么原因做出这样的评价呢？评价一个判断准确或不准确是很简单的：（1）我们在头脑中需要有一些可衡量的标准事件或情境作为判断的目标；（2）要确保做判断的人与我们对该判断目标的本质认识一致，而且与我们采用同样的标准来估计、预测和判断；（3）我们还要确保做判断的人希望预测的偏差最小化，且由于偏差的“代价”是对称的，因而判断者不会总是过高或过低地估计标准。[例如，本书的一个作者指出他对于熟人年龄（标准）的判断常常不准确，而且系统性地偏低。但你也要知道这种偏差带有一些故意的成分，是为了避免伤害那些对自己显老很敏感的人。]评估判断质量的这种逻辑被称为准确性方面的一致框架，这个框架是构成本书第3章所介绍的透镜模型的基础。（更多相关的讨论参见Hammond，1996或Hastie &Rasinski，1988。）

然而，我们也讨论了在无法明确使用一致性检验的情况下判断的非理性和不一致。例如，我们说，那些认为琳达更可能是“一位女权主义的出纳员”而非“一位出纳员”的人是非理性的，其判断有偏差，尽管没有一位真实的琳达存在，否则其职业和态度可以作为对判断准确性进行一致性检验的标准。在这样的例子中，我们评价判断的质量，只能将这种方法应用到两个或更多判断中，通过考虑它们之间的统一性或逻辑一致性来做出评价。逻辑规则和概率论是我们普遍接受的理性推理标准，我们常常参考它们来评价判断之间的一致性。此外，如果我们的一系列判断是不一致的，我们就能确信其中有一些判断是不准确的，尽管我们没法说出哪一个判断有偏误。（更普遍地说，正如第2章所言，自相矛盾无法构成对世界的真实描述。）

另一个能够帮助我们证明某些判断错误确实是非理性的理由是：在向实验被试展示他们的反应并告诉他们违反了规则之后，他们会马上总结说“我犯错了，”或者甚至是“哇，我真蠢，我都不好意思了”。Kahneman和Tversky（1982，1996）首先指出了我们所讨论过的大部分错误，他们将这些判断错误统称为错觉，因为这些偏差已然成为行为习惯，虽然当我们仔细思考后会知道自己犯错了，但当我们没有运用自我控制来抵抗这种本能趋势时，这些错误仍然会出现——很像那些我们所熟悉的但无法抗拒的视错觉。

深思熟虑地进行推理和出于自动反应而做出某种行为是不同的，对这两者的辨析是区分分析性推理和直觉性推理的基础（Kahneman，2003）。Seymour Epstein和他的学生（Denes-Raj & Epstein，1994）发现，仅仅通过引导实验被试回答“一个完全逻辑性思维的人会如何思考”这个问题，就能减少甚至消除Kahneman和Tversky提出的一些偏差（例如第5章的琳达问题及其他脑筋急转弯类型的概率问题）。他们给自己的文章起了个恰如其分的名字：《人们什么时候会与自己的最优判断作对》。然而，一般而言，仅仅引导某人“理性地做”，还不足以诱导出理性思维。

当我们致力于利用逻辑、数学和决策理论作为评价一个判断和选择是否理性的标准时，在实践中真正做到理性评价还需要更多的努力。第一，如何客观表征一个决策问题，以便可以应用理性原则，做到这一点并不总是那么容易。即使有清楚的文字描述，例如本章一开始所举的那个脑筋急转弯问题，我们对于所要分析情境的认识仍有不完整、模糊甚至矛盾之处。此外，明确个体在情境中的确切目标通常是困难的，大多数理性分析都需要知道决策者究竟最重视什么，以便定义一个理性的评价标准。因此，即使我们有很明确的理性标准，但判断一个决策是否非理性、以及非理性到什么程度仍是个问题。

第二，总是关注一个有充分信息、有足够时间来安静思考的人的短期行为表现并不合适。我们应该更关心人们在嘈杂的、有干扰的、信息不充分的环境中做出长期决策时的表现。在实际条件下，理想化的理性判断并非一定就是适应性的最佳判断。John Payne（Payne，Bettman，& Johnson，1993）、Lola Lopes和Gregg Oden（1991）及Gerd Gigerenzer（Gigerenzer，Todd，& the ABC Research Group，1999）所领导的一些学者近期探讨了这一话题。这些科学家认为，在判断和决策中，“快而省”的算法或启发式可能比理想化的计算更加稳健，更有生存价值；后者仅在信息、计算容量和时间都很充分的情况下才更有优势。

到目前为止，我们以导致判断出错的认知过程及启发式为线，阐述了前4章提到的判断错误，即已经完成了关于判断中“行为方面”的讨论。现在我们将要讨论的是违反概率规则和逻辑的判断错误，并且给出一些如何避免这些不理性判断的建议。我们必须告诫读者，推断一个判断过程到底先违反了哪一条概率论规则有时是困难的。因为这些规则互相关联，很难确切地指出哪个是首要错误——是对需要判断的事件中子集成员关系进行了错误地表征，还是错误地认为两个不同的可能性或不同概率是一样的，抑或是忽略了与判断有关的重要信息（如背景基础比率）等。

8.5 如何思考逆概率

由于人们（包括本书作者）不认真区分那些容易混淆的逆概率而导致判断出现偏差，对此我们已经给出了很多例子（参见章节5.10）。让我们花一些时间来详细分析一个具体的例子（来自于Gay McGee在1979年的一篇新闻报导）。

密歇根州海湾市，1979：本地有一名外科医生，查尔斯·罗杰斯博士，他是全国范围内采用先进疗法治疗乳腺癌的几位先驱之一，他们的做法是在肿瘤形成之前就切除有高患癌风险的乳房。

乳房X光透视中所呈现的乳导管和小叶的形态是判断是否存在发病风险的依据，属于高患癌风险组的女性中会有一半以上的人在40到59岁之间形成肿瘤。底特律放射学家约翰·沃尔夫博士开展了诸多如上所述利用X光透视检查乳房形态的研究。

被称为预防性乳房切除术的外科手术包括去除皮肤和胸腔之间的乳腺组织和乳头。

利用剩余皮肤进行乳房复原的工作通常与切除手术同时进行。按照医生的说法，植入硅胶和乳晕（乳头周围的深色皮肤）替代物，使术后的女性“看上去仍是个女人”。

他在两年内已经对90名女性实施了这一手术。

手术的基本原理基于外科医生对放射学家沃尔夫所做研究的解释。报纸中的文章在此处继续写道：

沃尔夫的研究发现，大众群体中每13名女性就有1名会患上乳腺癌，然而每2到3名DY型（高风险）女性中就会有1名在40到59岁之间患病。（斜体是后加的，沃尔夫并没发现这一点，他的发现在下一段叙述。）

低风险女性（NI型）占总体的42%，她们中只有7.5%的人会患上癌症。通过检查DY型女性和风险其次的P1和P2型，沃尔夫认为93%的乳腺癌可能在57%的人身上发现。

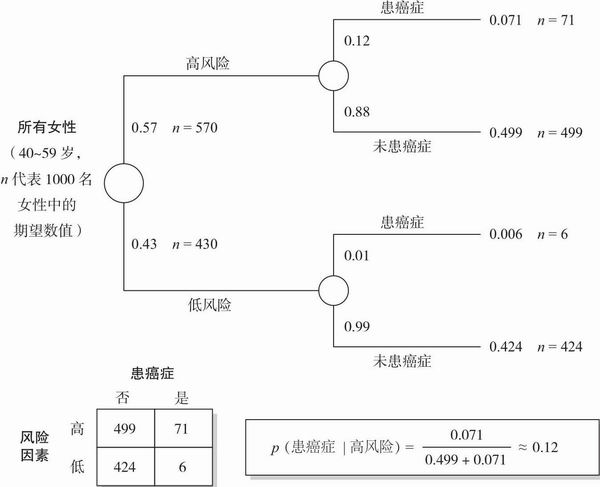
图8.3　表征罗杰斯乳腺癌问题的概率树

在此问题中，减少混淆的一个方法是将问题转换为系统的符号表征。将每一个需判断的情境转换为概率论符号，然后仔细地应用概率论的基本规则。（参见章节5.10对比例规则的讨论，更综合的讨论见附录概率论部分。）让我们来看看这一方法，将概率树表征应用于罗杰斯的例子。根据罗杰斯的数据，我们可以建立一个1000名典型女性的模型（见图8.3中的表格）。注意到499+71=570，即总体的57%，这个数字表示高风险组人群的比例。同样地，71/（71+6）= 0.92，表示92%的乳腺癌病例在57%的人口中被查出来。乳腺癌在总体中的患病率是（71+ 6）/1000 = 0.077。

让我们回到罗杰斯对乳腺癌的研究，尽管92%的癌症在高风险组被查出是真实的，但一个高风险组女性患癌症的估计概率只有71/570或 0.12。（别忘了这些计算都基于罗杰斯自己的数据。）

应用比例规则可以更容易算出0.12这个数字。根据沃尔夫的数据，p（癌症）= 0.075，p（高风险癌症）= 0.93，且p（高风险）= 0.58。因此

根据大量信息所得出的统计结论并不支持文章中医生的观点。根据上述数字，低风险组女性患上乳腺癌的估计概率是6 /（424+6），即0.014。基于这篇新闻报导是不可能得出DY组在患癌症上是高风险的结论。

罗杰斯博士并没有强调以上这个否定推论的价值。在强调所有超过30岁的女性都应该每年做乳房X光检查后，文章引述他的话说：“最大的危险在于做乳房X光时没有同时经由医生做医学检查。很多时候医生都检查出了X光没有反映的问题……这肯定是1+1大于3的一个例子”（McGee，1979）。

同意，但顺便说一句，他的X光检查建议同样也是基于对逆概率的混淆而做出的。大约20%的癌症没有被X光检查查出——即外科医生检查出了“X光没有反映的问题”。但这与检验中呈阴性（即正常）但其后患病的百分比有很大区别；p（癌症阴性）≠ p（阴性癌症）。事实上，在这篇文章写作时，根据哈佛保险计划刚刚完成并公布的数据，前一个数字大概是0.5%，也就是大部分人都不会认为这意味着“极大的危险”。（公平地讲，我们必须指出这篇文章没有明确说明高风险组患者在罗杰斯做手术前到底有多高风险。我们评论的要点是，从理性的角度来讲，他用于论证的整个推理过程是完全没有说服力的。）

一般而言，若要思考逆概率，文字不是个好的媒介。很显然，一些文字关联并不对称，例如，“玫瑰是红色的”并不意味着红色的花都是玫瑰。然而，其他的文字关联也有可能是对称的，“充满氢气的飞艇会爆炸”也可以说成“爆炸的飞艇充满了氢气”。我们很容易混淆对称和非对称的文字关联。事实上，语言关联常因其模棱两可而遭人诟病。（例如，“天空并非整天多云”意思是天空只在一部分时间多云，还是整天晴朗无云？）也有时候，人们用语言表达的信念是真诚的，但却未完全理解其意义。（多少学生唱美国国歌时将o’er正确理解成over而非or？或者有人问“摩西用方舟接走了多少种动物”时，会有多少人信心满满地回答“两种”，却并未注意到接走动物的不是摩西而是诺亚——《圣经》所记载洪水中乘坐方舟而幸存的人）

然而对于很多人来说，不用词汇思考是很困难的。事实上，一些卓越的思想家坚决认为不用词汇思考是不可能的：“我们如何知道头上有天空而且它是蓝色的？如果它没有名字我们还会知道它是天空吗？”（麦克斯·穆勒）；“语言由智慧所创造，并将创造智慧”（阿伯拉尔）；“人类的本质是语言”（《奥义书》）。“最初产生的是词汇”（《创世纪》第一章第一节）。但可能《楞伽经》的建议更加有用和正确：“信徒应该防范词汇和句子及其虚幻含义的诱惑，因为无知者和愚蠢者将因此陷入困境变得无助，就像大象在泥浆中挣扎。”也许我们应该培养非语言思维模式，就像爱因斯坦写道：“被写或说出来的词汇或者语言，似乎并没在我的思维机制中发挥任何作用。”不过，具体的、视觉的形象也并不总比文字好，图像也可能导致决策偏差。

符号，特别是代数表征是有效的，但很多人并不擅长代数。幸运的是，图像方法对表征概率问题和日常情境很有帮助。我们数次利用韦恩图来理清逻辑关系，特别是涉及条件概率的时候。但对于大多数问题，我们推荐使用决策树和概率树，因为它们的应用更加广泛，且能更有效地组织与决策问题有关的数字信息。

8.6 避免次可加性与合取谬误

当人们依靠相似性感知对涉及不同范畴的事件进行判断时，很容易出现另一个臭名昭著的习惯性偏差，即估计了几个独立事件概率之后，发现其概率相加超过100%。例如，你的汽车无法启动，这可能是由于电池故障、线路松动、输油管阻塞、油箱没油或安全带挡住了点火装置——这些可能性之和居然是1.55。在极端情况下，次可加性意味着单一子事件的概率大于上级事件（例如，琳达是一个女权主义银行出纳员的概率比她是银行出纳员的概率还大）。这个问题之所以被称为次可加性，是因为整体的概率小于各个部分概率之和——在合取谬误中，甚至小于其中某一单独部分的概率。

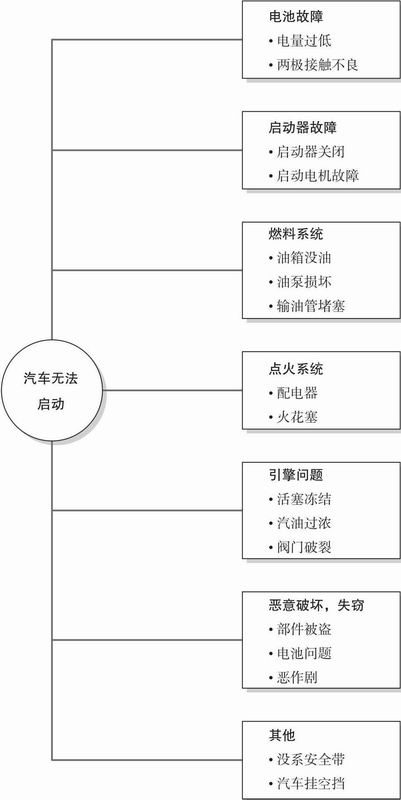
图8.4　表征汽车无法启动的一个似乎合理但并不完整的概率树（“故障树”）

如果我们用图表来表示“我的车无法启动的原因”中各个独立子事件的关系，我们就不太可能得出一个大于100%的概率空间，我们也会更加敏感地估计各种故障的基础概率（见图8.4）。事实上，在人们做多子事件决策时，仅仅口头提醒他们所有独立子事件的概率之和不能超过1.00（只要他们能正确使用概率数字），就能有效地引导他们做出更加理性的推理。Lori Van Wallendael和Hastie（1990）曾要求高校学生解决一些侦探推理谜题。如果没有提醒学生不同的、互相独立的犯罪嫌疑人犯罪概率之和应该为1的话，他们的推理就会表现出很大的次可加性。当发现一些新的犯罪证据时，他们会更加高估嫌疑人犯罪的可能性，但同时对其他嫌疑人的怀疑却不会降低。然而，如果提醒他们相互独立事件的概率像“水泵”一样有增就应该有减时，他们就会更加理性地权衡有罪与无罪的判断。

概率树和韦恩图表之类的表征（见图8.5）也能够减少合取谬误。在章节5.8中，我们注意到如果画一个韦恩图表来表示“银行出纳员”和“女权主义的银行出纳员”之间的关系，那么我们就不太可能认为“女权主义的银行出纳员”的概率高于“银行出纳员”。概率树也可以防止我们犯这些思维表征错误，而依据频率框架来思考这个问题更能消除思维中的偏差。86%的高校学生在一开始的概率框架中会犯“琳达是女权主义银行出纳员”问题的合取谬误，但当Klaus Fiedler（1982）再次用频率框架来说明这个问题时，错误率降低到约20%（例如“假设有100个人符合对琳达的描述，那么她们中有多少人是银行出纳员？多少人既是银行出纳员又是女权主义者呢？”）。

8.7 硬币的另一面：事件的析取概率

考虑一系列事件1、2、...、k。假设这些事件是独立的，即某一事件是否发生不影响其他事件的独自或联合发生。（独立性的更准确定义见附录。）假设这些事件都发生的概率（合取概率）是p1 × p2 × … × pk，那么至少一个事件发生的概率是多少？也就是说，这些事件的析取（disjunction）（与合取相对）概率是多少？析取概率等于1减去所有事件均不发生的概率。第一个事件不发生的概率是（1-p1），第二个事件不发生的概率是（1-p2），依此类推。因此，所有事件均不发生的概率是（1-p1）×（1-p2）× …（1-pk）（详见附录。）即使由于每个pi很小从而使得每个（1-pi）很大，其乘积的结果也可能非常小。例如，设六个事件的概率分别为0.10、0.20、0.15、0.20、0.15和0.10。那么（1-pi）乘积的结果为0.90 × 0.80 × 0.85 ×0.80 × 0.85 × 0.90 = 0.37，至少一个事件发生的概率即为1 – 0.37 = 0.63。尽管每个单一事件发生的概率都很小（平均为0.15），但其析取概率也可能较大。

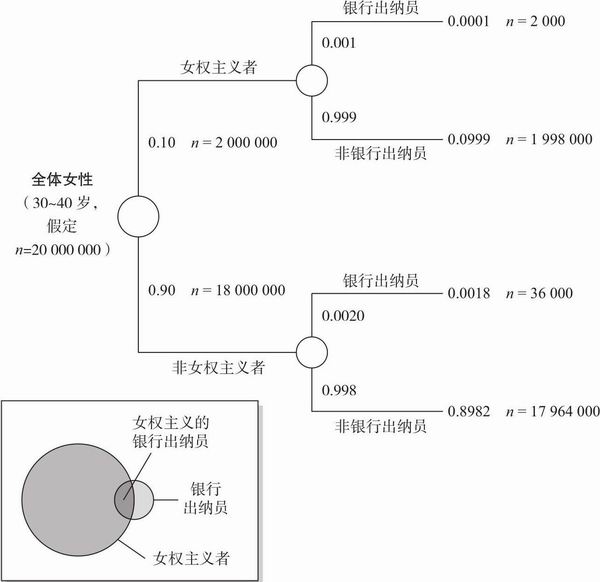
图8.5　表征女权主义银行出纳员琳达问题的概率树和韦恩图表（为了得到一个不精确但大体合理的频率，本图作了一些频率假设：美国人口中共有20 000 000名与琳达年龄相当的女性，一名女银行出纳员不是女权主义者的可能性比她是女权主义者的可能性高20倍，每1 000名女性中有2名是银行出纳员。）

就像我们倾向于高估事件的合取概率一样（合取概率谬误），我们也倾向于低估事件的析取概率。这可能有两个原因。第一，我们倾向基于单一事件概率进行判断；如上所示，尽管那些事件的概率都很小，但析取概率可能很大。我们将这种错误归因于“锚定-调整”的估计过程；第二，导致我们低估单一事件概率的任何非理性因素——例如该事件难以想象——可能会导致我们低估整体的析取概率。在有些情况下，这个低估的问题很直观、容易为人理解。例如，律师在总结时常常避免析取而趋向合取。（著名律师Richard “Racehorse” Haynes为说明“在选项中辩论”的错误而举了一个幽默的例子：“比如你控告我，说我的狗咬你。那么以下是我的辩护：第一，我的狗不咬人；第二，我的狗在夜晚是拴着的；第三，我不相信你真被咬了；第四，我没有狗。”[3]还有更一针见血的，比如辛普森的著名辩护：“我没有这样做；没有人看见我这样做；你无法证明任何事情。”）当然，从理性而言，析取事件发生比合取事件发生的可能性要大得多。

这里有一个与合取概率谬误类似的析取概率谬误的证据，即认为一个析取事件较其包含的单一事件来说更不可能发生（Bar-Hillel & Neter，1993）。然而，逻辑上讲，如果理所当然地认为A且B的概率大于A单独的概率（合取谬误），那么非A的概率就会小于非A或非B的概率。这是因为非A的概率是1减去A的概率，而非A或非B的概率是1减去A且B的概率。因此，前一个谬误必然导致了后一个。事实上，如果我们能够任意决定将什么称为A和非A（例如，称非女权主义者为A，女权主义者为非A）、B和非B（称非出纳员为B，出纳员为非B），那么这两个谬误的不等式难道不是一样的吗？我们的回答是，它们在逻辑上是等价的，但在心理上不相等。我们是基于类别思考，而非他们的补集（即对立面）。对于一个受过训练的逻辑学家来讲，非A就像A一样是定义明确的一个类别，但对我们而言A（可能有很多关联）充满了我们的脑海，非A（好像只有很少）却没有。我们需要一个福尔摩斯一样的头脑来想明白，“狗没有叫”这个事实构成了至关重要的线索（表明狗与犯人相当熟悉）。这就是说，将“没有叫”当做一个事件。

8.8 改变我们的想法：贝叶斯定理

在考察一个假设是否成立时，我们会不时接收到一些新的信息，这时，我们在判断中的一个常见问题就出现了。我们需要调整关于该假设成立可能性的判断。我们来看看内科医生感兴趣的一个问题，即医生和患者到底如何解读医学检查结果所呈现的新信息（Casscells，Schoenberger，& Graboys，1978）。

40岁以上妇女的乳腺癌患病率为1%。广为应用的X光透视检查会对10%未患乳腺癌的妇女报告出阳性结果，也对80%真正患乳腺癌的妇女报告出阳性结果。那么一个在此年龄段得到阳性检查结果的妇女，其真正患乳腺癌的概率是多少呢？（p.999）

当David Eddy（1988）问在一线工作的内科医生这个问题时，100人中居然有95人回答“大约75%”。这个估计错得离谱。对于这些每天都要做此类判断的内科医生而言，此判断反映了他们在真实情境下根据X光检查结果所做出的判断，这个错误的确太大了。正确答案是多少？大约7%——比那些内科医生的估计低了一个数量级！

计算正确答案需要用到代数方法。如果我们学习过概率论，那么不难看出下式可用于解决这个问题，附录提供了一个一般性（非正式）推导，参见附录A.5：

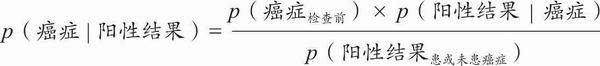
原问题为我们提供了需要代入等式右边的所有概率：p（癌症检查前）= 0.01；p（阳性结果癌症）= 0.80，p（阳性结果患或未患癌症）= 0.107。最后一项0.107这个数据需要一些计算才能得出：如果一个人患癌症（1%妇女属于此类），那么结果是阳性患有癌症的概率是0.008（= 0.01 × 0.80）；如果一个人未患癌症（99%妇女属于此类），那么阳性结果且未患癌症的概率是0.099（= 0.99 × 0.10）；因为人只可能患或未患癌症，那么我们将这两个概率相加即得结果，0.099+0.008 = 0.107。我们将所有数据代入等式右边，得：（0.01 × 0.80）/ 0.107，约为0.07。这个结果也可从更简单的式子得来： p（癌症阳性结果）× p（阳性结果）= p（癌症）× p（阳性结果癌症）。

这个有名又有用的公式用于解决在给定条件下调整判断的问题（比如更新了证据之后对某事件是否为真或是否会发生所做的判断）。它被命名为贝叶斯定理（Bayes’ theorem），以纪念Thomas Bayes——一位在得到（对他来说的）上帝有所做为的丰富证据以后试图以理性方法来评估上帝存在的概率时，以代数方法得出此公式的英国牧师。（令人惊讶的是，几乎所有本书的读者都能够在问题得到清晰陈述之后，用概率论四个基本法则推出这个深刻的定理；见附录。这个公式也能轻易地以概率树的形式表示；见图8.6，用概率树呈现Eddy癌症诊断问题。）

当人们收到新信息并试图更新关于该事件的看法和判断时，会产生什么系统偏差呢？我们要重复我们的忠告：通常很难指出判断过程中究竟哪一部分的错误是致命的，而将偏差归结为对概率论的特定误解或误用则更加困难。在Eddy的X光检查例子中，我们可以把错误描述成未能考虑到另外一种可能，忽视了即使假设不成立、支持假设的证据也可能出现的可能性——即上例中的p（阳性结果未患癌症）经常被忽略。关注凸显信息是我们在注意和推理时普遍存在的一个习惯；这甚至可以归因于那些可得到的凸显信息带来的普遍偏差，正是这种信息支配着我们的判断。（Nickerson，1998，提供了关于这种证实性偏差的全面介绍。）第二种错误是，忽视了单一事件发生的基础概率（例如，低估了走进诊所的人里只有1%的乳腺癌症患者这一事实——在我们知道检查结果之前）。

我们在这之前已经遇到过忽视基础概率的坏习惯，其中最明显的例子是章节5.8中的对Penelope主要研究领域判断的错误，以及对工程师和律师的职业判断的错误，人们之所以犯这些错误，是因为其判断依据的是对各种人的性格概述和社会刻板印象。但如果根据概率论而非心理学给这个错误赋予一个概念的话，我们会说这是由于人们忽视基础概率或对其利用不足。这里有Bar-Hillel（1980）提供的另一个例子，在这个例子中基础概率很显然被忽略了（再次提醒，在阅读本书关于每个例子的分析之前先做出你自己的判断）。

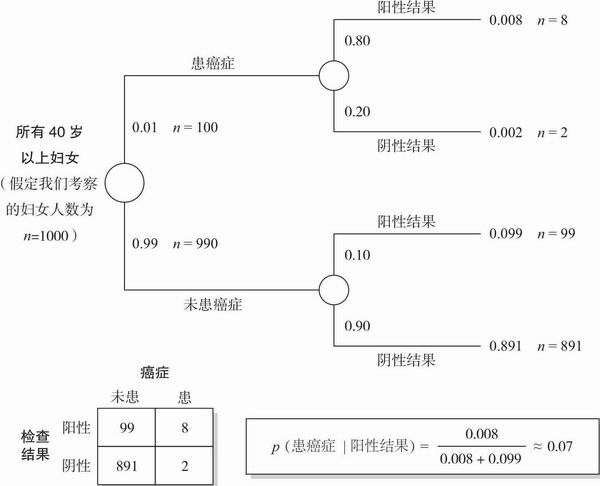
图8.6　表征Eddy癌症诊断问题的概率树和表格

某城有两个出租车公司，根据它们各自出租车的颜色，分别命名为蓝色和绿色公司。在所有出租车中85%的出租车是蓝色，15%的是绿色。

一辆出租车涉嫌一桩深夜肇事逃逸案。目击者事后确认那辆车是绿色的。法庭测试了该目击者在夜间视觉条件下辨别蓝色和绿色出租车的能力，发现他在80%的次数中能够正确辨别各种颜色，但20%的次数却与另一颜色混淆。

那么你认为肇事车辆如目击者所言是绿色的概率是多大呢？（p.211）

让我们将这些信息依据贝叶斯定理一一呈现：在此问题中，最重要的基础概率是道路上蓝色、绿色出租车的比例，这应该成为判断的起始点——在所有证据（例如目击者证词）呈现之前的“先验概率”。Bar-Hillel（1980）发现，当她将此问题呈献给不同群体的人时，人们普遍都忽视基础概率；当人们听到具体的目击证词时，基础概率便黯然遁入背景之中。于是，Bar-Hillel发现，典型的答案是目击者的正确率为0.80，人们并未根据基础概率信息进行调整。如果我们将这些数字代入贝叶斯定理的公式中（见图8.7），我们可以得到正确答案：0.41。

我们需要承认，上一问题的陈述有模糊之处：目击者是否在“15%绿色出租车”的条件下接受测试，从而使准确率已在后验概率的基础上得以调整？进一步讲，除了问题陈述中的信息以外还有其他解释，即读者可能将自身经验得来的关于出租车、交通事故、目击者等多种信息加入问题表征（例如，见Birnbaum，1983）。然而，并没有直接证据证实有人构想出这些备选表征，除了那些想通过考虑备选表征来批评Bar-Hillel结论的专家。事实上，本书作者之一（海斯蒂）收集的未发表数据大体与Bar-Hillel的解释一致，即大学生按照前面呈现的贝叶斯公式来理解这个问题，但忽略了基本概率信息。

如何补救这些错误呢？第一，我们在章节5.10中指出，在陈述问题时，若将基础概率与结果紧密联系在一起，特别当这种联系是因果关系时，人们更可能在决策中考虑基础概率。Bar-Hillel（1980）提出了一个关于出租车问题的新的表述：“警察的统计数据表明，在由出租车造成的交通事故中，15%的肇事车为绿色。”基于这个因果联系，大多数人表征问题时使用了基础概率来调整目击者识别的准确度（80%），尽管调整得并不充分（正如我们预期的那样）。这些发现也许可以证明，人们本能地倾向于依据情境中的因果关系进行判断是有其潜在道理的（见Krynski & Tenenbaum，2007）。我们推测，依据情境中的因果关系进行判断可能是人们弄清楚事件之间大部分重要关系的直觉性途径——当我们需要做预测、诊断或更新“情境模型”时，这条途径尤为重要。然而，仅靠自发的基于情境的推理并不够，当采用这种判断模式时，我们讨论过的大多数概率错误仍然存在。

图8.7　表征出租车辨别问题的概率树和表格

第二，利用如上所示的代数符号表征问题，会对判断的结果产生重大影响。现在在医疗诊断情境中会有软件为医生提供决策帮助，先询问医生对相关“先验概率”和“证据诊断力”的估计，然后计算事后概率。这些系统在重复的临床判断情境中改善了医生的判断，尽管医生的直觉推理和系统的反应形式间仍存在一些心理层面上的不匹配。人们仍然很难估计“假定条件或疾病不存在时仍发现证据（测试结果、目击者证词、症状等）”的条件概率。但如果一个要做判断的人能按照贝叶斯公式慎重地阐述问题并列出所有相关信息，其表现就会得到改善。即使这个人仅用这个公式来组织其思维而非用于计算，我们基于以下原因仍认为其会有行为表现的提升：（1）能够识别问题的不完全或模糊描述；（2）考虑到计算时所需要的不明显信息；（3）有动机去搜寻某些特殊信息以及去思考与假设不一致的信息（例如，假定出租车确为蓝色时目击者说“绿色”的概率；假定患者未患癌症但检查结果为阳性的概率；甚至嫌犯并非凶手但DNA检测匹配的概率）。

第三，也是最有帮助的，我们建议利用图表来表征情境，引导信息搜索、推断和计算，如图8.6和图8.7。要注意，按因果和时间顺序来画概率树通常是最好的。在X光检查诊断的情境中，先从40岁以上妇女的乳腺癌患病率为1%这个事实开始。然后，考虑X光检查可能会为10%未患乳腺癌和80%患有乳腺癌的女性给出阳性结果这个事实。那么，一位此年龄段的检出阳性结果的女性确实患有乳腺癌的概率是多少呢？最后，我们提醒大家从频率的角度来思考情境。例如，考虑1000个妇女接受了检查，然后遵循相关条件来进行思考。

连贯地、理性地进行概率推理不仅仅是一个课堂作业的问题。我们会越来越多地遇到那些在法院、医院、金融机构中以概率数值呈现的概率证据。想想看在辛普森刑事和民事审判中关于DNA匹配、血型证据的旷日持久的争论——或者下面某女记者在其乳房内发现肿块后向她的外科医生们咨询的故事（Kushner，1976）：

“我希望你去做个X光检查。这是乳房检查的一种新方法。”

“这方法准吗？”

他耸了耸肩，“可能跟其他片子的准确率差不多吧，你知道的”。接着，他警告说：“即使结果是阴性，就是说肿块不是恶性的，想要确认的唯一办法还是切除肿块然后在显微镜下查看。”

于是，这位妇女与她的丈夫讨论了一会儿这个问题。

“医生说了什么？”

“他希望我做一个X光检查，之后，无论结果如何，都要把肿块切除。”

“那干嘛还要先做X光啊？”

“这得按顺序吧，我觉得。医生说85%的时候它都是准确的……所以，我们先安排个时间去做个热谱图。无论结果是阴性还是阳性，无论它和X光片的结果是否一样，统计上说检查结果有95%的可靠性。”

有没有可能这位患者不必做检查呢？或者有没有可能无论检查结果如何她都不需要去做肿块活体检查呢？

8.9 统计决策理论

我们对不确定条件下估计和判断的讨论引出了一个重要的理论性和现实性问题：我们应该如何利用判断来决定是否采取行动？通常统计决策理论会提供“应该做”的规范化答案。（我们只能展示该理论的重要而精巧的部分；其余可参见Macmillan & Creelman，2004；Swets，Dawes，& Monahan，2000）。让我们来考虑一个简单的例子，一位医生评估病人患有严重疾病（如癌症）的概率并决定是否手术。（如今，这通常是由医患双方共同决定，尽管大多数病人希望医生替他们决策。）图8.8是描述这一情境的散点图，表征了很多相似患者接受这种判断的情形。这种呈现方式可以总结数百万个决定，其关键问题是：“多高的概率才能促使我们必须采取行动？”接受或拒绝、投资或不投资、进入或退出、转手或不转手、报复或不报复，等等。

“我必须采取行动吗？”这一问题的答案基于这些概率（与你现有知识和需要推断的真实情况有关）以及你对四种可能结果中的每一种到底有多重视。（提醒一下，在这个简单但现实的例子中，如果我们能够确定真实情况是什么，我们当然知道如何做；但由于存在不确定性，我们不得不面临艰难的选择。）进一步讲，如果我们知道该如何评价结果，我们就可以退回来计算一个规定行动与否的概率阈限，以便获得最大化价值。

图8.8给四种可能的判断结果赋予了广为人知的称谓：（1）击中（hit）或正确肯定（true positive），意味着正确判断出目标条件，如正确判断了癌症事件； （2）未击中（miss）或错误否定（false negative），意味着错误的作出患者没有患病的判断；（3）虚假警报（false alarm）或错误肯定（false positive），意味着错误作出患者患病的判断；（4）正确拒绝（correct rejection）或正确否定（true negative），意味着正确判断出患者没有患病。（这张图描述的情景是，在200人中，30人真的患有癌症，170人是健康的，而医生诊断与患病与否之间的相关接近+0.65。）

从散点图中立即可得到的一个发现是，我们通过改变是否决定要做手术的阈限，就能够控制多种判断结果出现的比率。如果我们将手术阈限设为当判断患癌症概率是0.60时，我们看到15例击中，但也有15例未击中（即占总体7.5%；30例患癌症者中的15例，即50%未击中），但我们的代价是较多的虚假警报（即不必要的手术——总体10%；35例中的20例，占到实施手术的57%）。如果我们将阈限降低到当判断p（癌症）为0.50时，我们会提高击中至20例，减少未击中到10例，但代价是更多的虚假警报（30例，或总体的15%）。

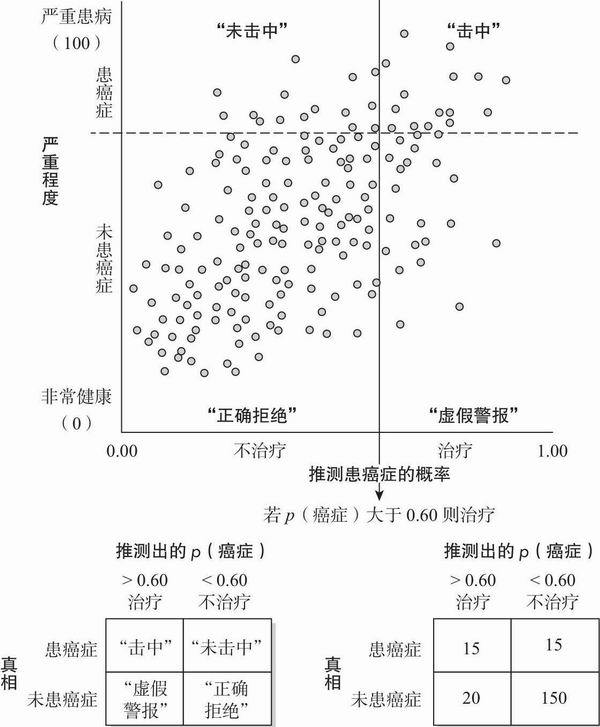
图8.8　统计决策理论图表（此图表征了不确定性下的医疗决策，医生判断患者患有癌症的概率，并基于其判断结果决定是否医治患者。此处假设以健康状况不同的200名患者来表征该问题。判断是中等准确的，判断与真实健康状况的相关为r = 0.65。判断方法是，若p（癌症）大于0.60，则决定治疗该患者；根据统计决策理论中的“击中”“未击中”“虚假警报”“正确拒绝”概念，针对200名患者的判断和结果总结在图下面的表格中。警告：统计决策理论的不同应用需要不同的总结表格；此处的表征与心理学信号检测论的惯例一致，后者是统计决策理论的一个有效版本。）

似乎很多政策讨论都忽视了非常重要的一点：很多时候，仔细思考我们重视什么，最想避免哪种错误，就能提高决策水平。我们通常无法提高诊断或其他判断的准确率（在这个例子中，我们无法提高医生的诊断准确率），但我们却能权衡两种错误（也包括“正确”）。如果未击中的代价更高，我们可以降低决策阈限以便减少未击中（但代价是更多虚假警报）；如果虚假警报是更严重的问题，我们就可以提高决策阈限以减少虚假警报（当然代价是更多未击中）。我们常常通过提高准确率来试图避免这些悲剧性的权衡，这样两种类型的错误率都会下降。因此，这就是为何我们每年花费数十亿美元来提高医疗、军事、金融和气象预报的准确性的原因所在。但是，几乎不存在什么政策情形能使我们能消除所有的不确定性。在大多数情况下，我们必须认识到我们总面临着权衡和取舍，必须明智地讨论我们看重什么，再据其设定决策阈限（Hammond，1996）。

如果我们面临权衡取舍，我们就要评估多个“判断-结果”，之后应用统计决策理论来确定一个合适的决策阈限。例如，假设数字+100，0，+30，和+80分别代表四种结果对于我们的价值（击中、未击中、虚假警报、正确拒绝；价值的取值范围约定俗成为0~100）。需要注意的是，对于不同人，这些价值可能有显著的差异。一位患者可能最看重“击中”的价值，但最不看重“未击中”（就如我们在价值量表上的排序一样），但一个政策制定者可能更看重“正确拒绝”而更厌恶“虚假警报”。我们的例子假定了单一的数字价值，我们可以据此计算出使价值函数取最大值的决策阈限。在这个例子中，当设置决策阈限p（癌症）接近0.55时，取得最大化的总体价值（因为计算过程涉及到微积分，故而省略）。

于是，在很多实际情境中，我们应该更努力地思考价值，而非准确率。但决定价值是一个复杂的过程，即便只涉及一个决策者（见下两章），这是因为日常选项经常是多属性且多目的的。我们在进行组织或社会政策分析时，必须综合分析具有不同个人价值取向的利益相关者，这样任务就会更加令人畏惧。然而，这些困难不应该成为我们更努力、更系统地思考的阻碍，我们应当从不同角度思考那些无法避免的权衡取舍。

8.10 关于理性的总结

如果一个科学理论无法说明事件何时发生，那么怀疑者就会问：这理论有什么用？事实上，一个彻头彻尾的行为主义者（如果还存在的话）可能会批评这整本书，因为既然我们讨论的现象都无法控制，那么对它们的描述（和假设的机制）是没有科学价值的。我们的回答是，到目前为止，我们在处理繁杂而令人困惑的真实世界中人们的心理事件和决策时，我们既无法完美地预测它们，又无法完美地控制它们。所谓“其他条件相同”的限定条件也常常证明了这一现象。预测实际结果时存在的不确定性，对于决策问题本身以及决策结果而言都是无法避免的。当然，可能有人会说，真正的科学家不应该研究这些不确定的现象，而应该仅限于研究环境中只有一个杠杆可动时，老鼠按压杠杆的比率。（除了操控惟一能够被操控的设置所产生的结果，还有什么能改变老鼠的行为呢？）但若所有科学家都按照这个法则待在象牙塔里，我们就不会有气象学、农学、遗传咨询、计算机科学，还有许多其他实用的应用科学了。

当然了，完全理性的思维过程不保证一定可以获得真实结论，还必须有实际、有效的信息输入。当海斯蒂第一次讲授他的判断与决策课程时，他在满教室20多岁的年轻人中发现了一位中年学生。过了几节课，那位中年学生做了自我介绍并解释了为什么会选这门课程。就如那位学生所述，他遭受了一系列不幸，处于离婚和即将失业的阴影之中。他说，最初他非常困惑，为什么这些事情会发生在他身上，但经过深思，他意识到他实际上只是一个庞大的“心理学实验”中的一个被试。（事实上，他来哈佛学习的一个原因是他想要见B.F.斯金纳教授，他相信斯金纳教授就是控制他生活的实验者。）他又引用了几十个难以解释的行为和事件，只有当他假设自己真的“在一个心理学实验”中才能够解释这一切。海斯蒂想要他提供具体的例子，但他提出的证据都不够有力，因为大多数例子在其他的假设下（即那位学生并不处在心理学实验中）也有可能发生（例如，“我妻子打断我的话，然后正好说出了我之前想要说的话”；“我下班后和同事正在喝酒，他说起公司正在裁员，仅仅几天之后我就被炒鱿鱼了”）。不过，他的这一妄想系统的积极一面是，他相信这场实验最终会结束并公之于众，相信他已然显露的天资（由于被实验者所控制）将证明他有做领导的品质，能够在政府高层担任可靠的领导。

可能这则轶事最吸引人的部分是那位学生对于为什么接近海斯蒂所做的解释：他担心自己由于对这些事件的解释不理性而被欺骗。因此，为保证他不得到一个错误结论，他试图尽可能小心谨慎地应用老师的忠告。选了海斯蒂的课之后，他意识到他需要慎重地运用贝叶斯定理，参考他收集到的诸多证据，来评估“我是一场庞大而神秘的心理学实验的被试”这一假设的后验概率。他在评估假设的计算方面希望得到帮助！

这个故事在那一学期并未结束。几个月后，那位同学拜访了海斯蒂，希望后者能在自己保住工作的诉讼中作证。但其雇主的精神科医生已经诊断其患有严重的偏执妄想（海斯蒂觉得可能是真的）；认为贝叶斯定理是他妄想系统的一部分，而且医生还认为托马斯·贝叶斯教士是其精神分裂症所导致的一个虚幻角色。（海斯蒂郑重反对那位精神分析师关于托马斯·贝叶斯是幻觉的断言，尽管他也很怀疑那999999/1000000的后验概率以及那位学生是某庞大社会实验的被试这些结论。当然，准备证词的经历也使得海斯蒂怀疑，自己与这个模糊的历史人物的交集仅仅只有一个以其名字命名的概率定理，为什么自己就这样坚信其存在。）“如果输入的是错觉，那输出的也必然是错觉。”——无论两者之间经过多么严密的计算。

我们一直致力于指出那些导致我们所有人做出非理性判断和选择（在非理性判断的基础上）的因素和思维方式。人们未必要陷入这些思维过程，如同一个惊慌的游泳者并不需要拼命将头伸出水面。像游泳者的生存训练一样，我们能够学会对抗这种本能反应而变得更加理性，但与游泳的例子一样，这需要知识、自控和努力。然而，从一个规范的角度而言，学会区分哪些情形会促进或阻止特定的行为、哪些思维方式是有效的或无效的，这都是心理学家和其他社会科学家十分重要的成就。

最后，我们要指出的是，那些试图掌握全部情境以便准确预测或控制的人，很少能比得上另外一些人，后者会在无法减少不确定性，而这些不确定性又起决定作用的情形下寻求适度目标。一个人试图理解所有的事情，却往往会一无所知。理解了思维的非理性并非一无是处，即使我们无法准确预测非理性何时出现，也并不总能知道如何控制它。

参考文献

Bar-Hillel, M.(1980).The base-rate fallacy in probability judgments.Acta Psychologica, 44, 211–233.

Bar-Hillel, M., & Falk, R.(1982).Some teasers concerning conditional probabilities.Cognition, 11(2), 109–122.

Bar-Hillel, M., & Neter, E.(1993).How alike is it versus how likely is it: A disjunction fallacy in probability judgments.Journal of Personality and Social Psychology, 65, 1119–1131.

Bennett, D.J.(1998).Randomness.Cambridge, MA: Harvard University Press.

Birnbaum,M.H.(1983).Base rates in Bayesian inference: Signal detection analysis of the cab problem.American Journal of Psychology, 96, 85–94.

Brase, G.L., Cosmides, L., & Tooby, J.(1998).Inpiduation, counting, and statistical inference: The role of frequency and whole-object representations in judgment under uncertainty.Journal of Experimental Psychology: General, 127, 3–21.

Casscells,W., Schoenberger, A.,&Graboys, T.B.(1978).Interpretation by physicians of clinical laboratory results.New England Journal of Medicine, 299(18), 999–1001.

Denes-Raj, V.,&Epstein, S.(1994).Conflict between intuitive and rational processes: When do people behave against their own better judgment.Journal of Personality and Social Psychology, 66, 819–829.

Eddy, D.(1988).Variations in physician practice: The role of uncertainty.In J.Dowie & A.S.Elstein (Eds.), Professional judgment: A reader in clinical decision making (pp.200–211).Cambridge, UK: Cambridge University Press.

Fiedler, K.(1982).Causal schemata: Review and criticism of research on a popular construct.Journal of Personality and Social Psychology, 42, 1001–1013.

Gigerenzer, G., & Hoffrage, U.(1995).How to improve Bayesian reasoning without instruction: Frequency formats.Psychological Review, 102, 684–704.

Gigerenzer, G., Todd, P.M., & the ABC Research Group.(1999).Simple heuristics that make us smart.New York: Oxford University Press.

Hammond, K.R.(1996).Human judgment and social policy: Irreducible uncertainty, inevitable error, unavoidable injustice.New York: Oxford University Press.

Hastie, R., & Rasinski, K.A.(1988).The concept of accuracy in social judgment.In D.Bar-Tal & A.W.Kruglanski (Eds.), The social psychology of knowledge (pp.193–208).Cambridge, UK: Cambridge University Press.

Kahneman, D.(2003).A perspective on judgment and choice: Mapping bounded rationality.American Psychologist, 58, 697–720.

Kahneman, D., & Lovallo, D.(1993).Timid choices and bold forecasts: A cognitive perspective on risk-taking.Management Science, 39, 17–31.

Kahneman, D., & Tversky, A.(1982).On the study of statistical intuitions.Cognition, 11, 123–141.

Kahneman, D., & Tversky, A.(1996).On the reality of cognitive illusions.Psychological Review, 103, 582–591.

Koriat, A., Lichtenstein, S., & Fischhoff, B.(1980).Reasons for confidence.Journal of Experimental Psychology: Human Learning and Memory, 6, 107–118.

Krynski, T.R., & Tenenbaum, J.B.(2007).The role of causality in judgment under uncertainty.Journal of Experimental Psychology: General, 136, 430–450.

Kushner, R.(1976, March 24).Breast cancer—the night I found out.San Francisco Chronicle, p.C1.

Laplace, P.S.(1951).A philosophical essay on probabilities (F.W.Truscott & F.L.Emory, Trans.).New York: Dover.(Original work published 1814)

Lopes, L.L., & Oden, G.D.(1991).The rationality of intelligence.In E.Eels & T.Maruszewski (Eds.), Poznan studies in the philosophy of the sciences and humanities (Vol.21, pp.225–249).Amsterdam: Rodopi.

Macmillan,N.A.,&Creelman, C.D.(2004).Detection theory: A user’s guide (2nd ed.).Mahwah, NJ: Lawrence Erlbaum.

McGee, G.(1979, February 6).Breast surgery before cancer.Ann Arbor News, p.B 1 (reprinted from the Bay City News).

Meehl, P.E.(1986).Causes and effects of my disturbing little book.Journal of Personality Assessment, 50, 370–375.

Nickerson, R.S.(1996).Ambiguities and unstated assumptions in probabilistic reasoning.Psychological Bulletin, 120, 410–433.

Nickerson, R.S.(1998).Conirmation bias: A ubiquitous phenomenon in many guises.Review of General Psychology, 2, 175–220.

Payne, J.W., Bettman, J.R., & Johnson, E.J.(1993).The adaptive decision maker.New York: Cambridge University Press.

Sedlmeier, P.(1997).BasicBayes: A tutor system for simple Bayesian inference.Behavior Research Methods, Instruments, & Computers, 29, 328–336.

Sedlmeier, P., & Betsch, T.(2002).Etc.: Frequency processing and cognition.New York: Oxford University Press.

Swets, J.A., Dawes, R.M., & Monahan, J.(2000).Better decisions through science.Scienti c American, 283 (4), 70–75.

Van Wallendael, L.R., & Hastie, R.(1990).Tracing the footsteps of Sherlock Holmes: Cognitive representations of hypothesis testing.Memory & Cognition, 18, 240–250.

Vos Savant, M.(1991, February 17).Ask Marilyn.Parade Magazine, 12.

[1] 塞壬是希腊神话中半人半鸟的海上女妖，常用美妙的歌声诱惑过路的航海者而使航船触礁沉没。英雄尤利塞斯率领船队经过墨西拿海峡的时候，因为事先得知塞壬的致命诱惑，所以命令水手用蜡封住各自的耳朵，并将自己绑在船的桅杆上，方才安然渡过。——译者注

[2] 拉普拉斯（1749~1827），天体力学的主要奠基人，天体演化学的创立者之一，分析概率论的创始人，应用数学的先躯。——译者注

[3] 越往后，论点越趋向于一个“合取事件”，越难以被推翻。——译者注